|
|
|
|
Zero-offset migration |
|
|---|
|
yaxun
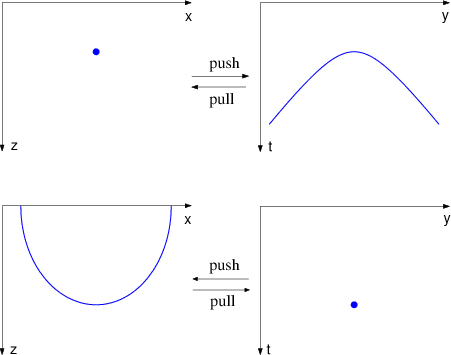
Figure 5. Point response model to data and converse. |
|
|
Now let us think backwards.
Suppose we survey all day long and record no echos except for
one echo at time ![]() that we can record only at location
that we can record only at location ![]() .
Our data plane is thus filled with zero values except the one
nonzero value at
.
Our data plane is thus filled with zero values except the one
nonzero value at ![]() .
What earth model could possibly produce such data?
.
What earth model could possibly produce such data?
An earth model that is a spherical mirror with bottom at
![]() will produce a reflection at only one point
in data space. Only when the source is at the center
of the circle will all the reflected waves return to the source.
For any other source location, the reflected waves will
not return to the source.
The situation is summarized in Figure 5.5.
will produce a reflection at only one point
in data space. Only when the source is at the center
of the circle will all the reflected waves return to the source.
For any other source location, the reflected waves will
not return to the source.
The situation is summarized in Figure 5.5.
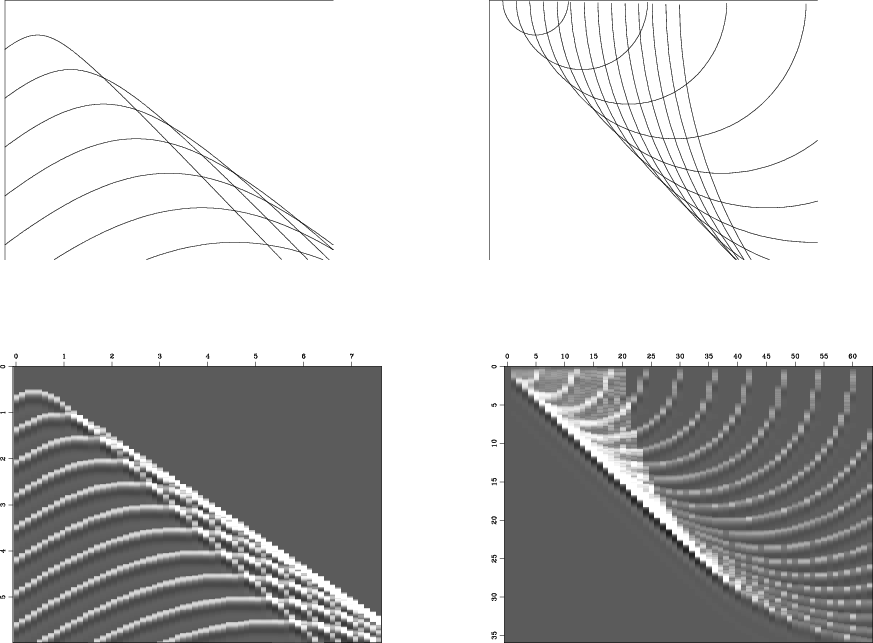
Above explains how an impulse at a point in image space can transform to a hyperbola in data space, likewise, on return, an impulse in data space can transform to a semicircle in image space. We can simulate a straight line in either space by superposing points along a line. Figure 5.6 shows how points making up a line reflector diffract to a line reflection, and how points making up a line reflection migrate to a line reflector.
|
|---|
|
dip
Figure 6. Left is a superposition of many hyperbolas. The top of each hyperbola lies along a straight line. That line is like a reflector, but instead of using a continuous line, it is a sequence of points. Constructive interference gives an apparent reflection off to the side. Right shows a superposition of semicircles. The bottom of each semicircle lies along a line that could be the line of an observed plane wave. Instead the plane wave is broken into point arrivals, each being interpreted as coming from a semicircular mirror. Adding the mirrors yields a more steeply dipping reflector. |
|
|
First we will look at the simplest, most tutorial migration subroutine I could devise. Then we will write an improved version and look at some results.
|
|
|
|
Zero-offset migration |