 |
 |
 |
 | Noncausal  -
- -
-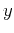 regularized nonstationary prediction filtering for random noise attenuation on 3D seismic data
regularized nonstationary prediction filtering for random noise attenuation on 3D seismic data |  |
![[pdf]](icons/pdf.png) |
Next: Synthetic examples
Up: Methodology
Previous: The review of -
Two dimensional  -
- NRNA only considers one space coordinate x. If we use
NRNA only considers one space coordinate x. If we use  -
- NRNA on 3D seismic cube, we usually apply
NRNA on 3D seismic cube, we usually apply  -
- RNA in one space slice.
RNA in one space slice.  -
- NRNA
reduces the effectiveness because the plane event in 3D cube is predictable along
different directions rather than only one direction. Therefore, we should develop
3D
NRNA
reduces the effectiveness because the plane event in 3D cube is predictable along
different directions rather than only one direction. Therefore, we should develop
3D  -
- -
-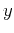 NRNA to suppress random noise for 3D seismic data.
NRNA to suppress random noise for 3D seismic data.

|
|---|
fig1
Figure 1. The  -
- -
-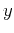 prediction filter. The trace
prediction filter. The trace
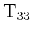 is predicted from circumjacent traces
is predicted from circumjacent traces
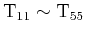 (except itself
(except itself
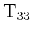 ).
).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
Next, we use Fig. 1 to illustrate the idea of  -
- -
-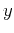 NRNA. The middle trace
NRNA. The middle trace
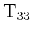 is the one we want to predict. Trace
is the one we want to predict. Trace
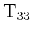 can be predicted from circumjacent traces
can be predicted from circumjacent traces
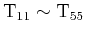 (except
itself
(except
itself
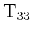 ). The prediction process includes all different directions.
For example, if we use
). The prediction process includes all different directions.
For example, if we use
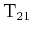 to predict
to predict
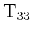 , we can
estimate a corresponding coefficient using the described algorithm in the following.
, we can
estimate a corresponding coefficient using the described algorithm in the following.  -
- -
-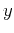 NRNA uses all around traces to predict the middle trace. Therefore, the prediction uses more
information than
NRNA uses all around traces to predict the middle trace. Therefore, the prediction uses more
information than  -
- NRNA. For all the traces in 3D cube, similar to the trace
NRNA. For all the traces in 3D cube, similar to the trace
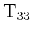 ,
we can use circumjacent traces to predict them. Mathematically, we can write the prediction process as
,
we can use circumjacent traces to predict them. Mathematically, we can write the prediction process as
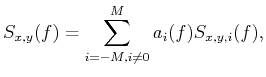 |
(4) |
where M and i are the number and index of circumjacent traces, respectively. In the case of Fig. 1,
M=24 and i is from 1 to 24. Note that
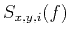 indicates the 24 circumjacent traces around
indicates the 24 circumjacent traces around
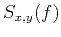 . Eq. 4 is the equations of noncausal regularized stationary autoregression.
Similarly to
. Eq. 4 is the equations of noncausal regularized stationary autoregression.
Similarly to  -
- NRNA, considerng the nonstationary case, we can obtain
NRNA, considerng the nonstationary case, we can obtain
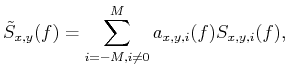 |
(5) |
where
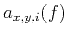 is the space-varying coefficients, which means they have three free degrees,
space axis x, space axis y and shift axis i.
is the space-varying coefficients, which means they have three free degrees,
space axis x, space axis y and shift axis i.
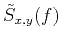 can be regarded as the
estimation of noise-free signal. However, the coefficients
can be regarded as the
estimation of noise-free signal. However, the coefficients
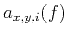 are not
known. Once we obtain the coefficients, we can estimate the effective signal using
Eq. 5 Similar to
are not
known. Once we obtain the coefficients, we can estimate the effective signal using
Eq. 5 Similar to  -
- NRNA, we use shaping regularization to solve this ill-posed
problem. Here, we assume that the coefficients
NRNA, we use shaping regularization to solve this ill-posed
problem. Here, we assume that the coefficients
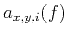
 -
- -
-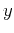 RNA are
smooth along two space axes x and y, which is reasonable because the curved surface
event in 3D seismic data is locally plane. Therefore, we can obtain the following
least square problem with shaping regularization
RNA are
smooth along two space axes x and y, which is reasonable because the curved surface
event in 3D seismic data is locally plane. Therefore, we can obtain the following
least square problem with shaping regularization
![$\displaystyle \min_{a_{x,y,i}(f)}\vert\vert{{S}_{x,y}}(f)-\sum\limits_{i=-M,i\ne 0}^{M}{{{a}_{x,y,i}}(f){{S}_{x,y,i}}(f)}\vert\vert _{2}^{2}+R[{{a}_{x,y,i}}(f)],$](img31.png) |
(6) |
where R[.] denotes shaping regularization term which constrains coefficients
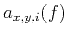 to be smooth along space axes. We use one coefficient with a given frequency and a given shift
(e.g., from
to be smooth along space axes. We use one coefficient with a given frequency and a given shift
(e.g., from
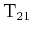 to
to
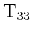 indicated by arrow in Fig. 1) to
explain the constraint in Eq. 6. This 3D cube of coefficient with a given frequency and a
given shift can be expressed as
indicated by arrow in Fig. 1) to
explain the constraint in Eq. 6. This 3D cube of coefficient with a given frequency and a
given shift can be expressed as
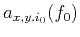 , which is smooth along
with variables x and y. The smooth constraint of coefficients is the objective of shaping
regularization. Finally, we use Eq. 6 to obtain obtain the complex coefficients of
, which is smooth along
with variables x and y. The smooth constraint of coefficients is the objective of shaping
regularization. Finally, we use Eq. 6 to obtain obtain the complex coefficients of  -
- -
-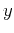 RNA, and use Eq. 5 to achieve the estimation of signal.
RNA, and use Eq. 5 to achieve the estimation of signal.
Transform-base methods can also be used for seismic noise attenuation (Ma and Plonka, 2010). Tang and Ma (1991)
proposed to total-variation-based curvelet shrinkage for 3D seismic data denoising
in order to suppress nonsmooth artifacts caused by the curvelet transform. Because the  -
- -
-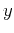 NRNA method uses shaping regularization to solve the ill-posed inverse problem and is
complemented in frequency domain, it has higher computation efficiency than curvelet-based methods.
NRNA method uses shaping regularization to solve the ill-posed inverse problem and is
complemented in frequency domain, it has higher computation efficiency than curvelet-based methods.
 |
 |
 |
 | Noncausal  -
- -
- regularized nonstationary prediction filtering for random noise attenuation on 3D seismic data
regularized nonstationary prediction filtering for random noise attenuation on 3D seismic data |  |
![[pdf]](icons/pdf.png) |
Next: Synthetic examples
Up: Methodology
Previous: The review of -
2013-11-13
![]() -
-![]() NRNA only considers one space coordinate x. If we use
NRNA only considers one space coordinate x. If we use ![]() -
-![]() NRNA on 3D seismic cube, we usually apply
NRNA on 3D seismic cube, we usually apply ![]() -
-![]() RNA in one space slice.
RNA in one space slice. ![]() -
-![]() NRNA
reduces the effectiveness because the plane event in 3D cube is predictable along
different directions rather than only one direction. Therefore, we should develop
3D
NRNA
reduces the effectiveness because the plane event in 3D cube is predictable along
different directions rather than only one direction. Therefore, we should develop
3D ![]() -
-![]() -
-![]() NRNA to suppress random noise for 3D seismic data.
NRNA to suppress random noise for 3D seismic data.

![]() -
-![]() -
-![]() NRNA. The middle trace
NRNA. The middle trace
![]() is the one we want to predict. Trace
is the one we want to predict. Trace
![]() can be predicted from circumjacent traces
can be predicted from circumjacent traces
![]() (except
itself
(except
itself
![]() ). The prediction process includes all different directions.
For example, if we use
). The prediction process includes all different directions.
For example, if we use
![]() to predict
to predict
![]() , we can
estimate a corresponding coefficient using the described algorithm in the following.
, we can
estimate a corresponding coefficient using the described algorithm in the following. ![]() -
-![]() -
-![]() NRNA uses all around traces to predict the middle trace. Therefore, the prediction uses more
information than
NRNA uses all around traces to predict the middle trace. Therefore, the prediction uses more
information than ![]() -
-![]() NRNA. For all the traces in 3D cube, similar to the trace
NRNA. For all the traces in 3D cube, similar to the trace
![]() ,
we can use circumjacent traces to predict them. Mathematically, we can write the prediction process as
,
we can use circumjacent traces to predict them. Mathematically, we can write the prediction process as
![]() -
-![]() -
-![]() NRNA method uses shaping regularization to solve the ill-posed inverse problem and is
complemented in frequency domain, it has higher computation efficiency than curvelet-based methods.
NRNA method uses shaping regularization to solve the ill-posed inverse problem and is
complemented in frequency domain, it has higher computation efficiency than curvelet-based methods.