 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: Damped solution
Up: UNIVARIATE LEAST SQUARES
Previous: UNIVARIATE LEAST SQUARES
Think of any real numbers 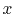 ,
, 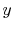 , and
, and 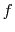 and any
program containing
and any
program containing 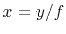 .
How can we change the program so that it never divides by zero?
A popular answer is to change
.
How can we change the program so that it never divides by zero?
A popular answer is to change 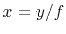 to
to
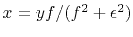 , where
, where 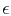 is any tiny value.
When
is any tiny value.
When
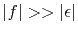 ,
then
,
then 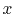 is approximately
is approximately 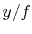 as expected.
But when the divisor
as expected.
But when the divisor 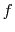 vanishes,
the result is safely zero instead of infinity.
The transition is smooth,
but some criterion is needed to choose the value of
vanishes,
the result is safely zero instead of infinity.
The transition is smooth,
but some criterion is needed to choose the value of 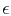 .
This method may not be the only way or the best way
to cope with
zero division,
but it is a good method,
and permeates the subject of signal analysis.
.
This method may not be the only way or the best way
to cope with
zero division,
but it is a good method,
and permeates the subject of signal analysis.
To apply this method in the Fourier domain,
suppose that 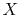 ,
, 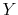 , and
, and 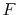 are complex numbers.
What do we do then with
are complex numbers.
What do we do then with 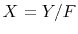 ?
We multiply the
top and bottom by the complex conjugate
?
We multiply the
top and bottom by the complex conjugate 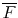 ,
and again add
,
and again add 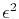 to the denominator.
Thus,
to the denominator.
Thus,
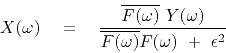 |
(1) |
Now,
the denominator must always be a positive number greater than zero,
so division is always safe.
Equation (1) ranges continuously from
inverse filtering, with
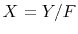 , to filtering with
, to filtering with
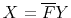 ,
which is called ``matched filtering.''
Notice that for any complex number
,
which is called ``matched filtering.''
Notice that for any complex number 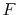 ,
the phase of
,
the phase of 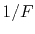 equals the phase of
equals the phase of 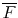 ,
so the filters
have the same phase.
,
so the filters
have the same phase.
 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: Damped solution
Up: UNIVARIATE LEAST SQUARES
Previous: UNIVARIATE LEAST SQUARES
2014-12-01
![]() ,
, ![]() , and
, and ![]() are complex numbers.
What do we do then with
are complex numbers.
What do we do then with ![]() ?
We multiply the
top and bottom by the complex conjugate
?
We multiply the
top and bottom by the complex conjugate ![]() ,
and again add
,
and again add ![]() to the denominator.
Thus,
to the denominator.
Thus,