Next: Computational part
Up: Homework 1
Previous: Prerequisites
You can either write your answers on paper or edit them in the file
hw1/paper.tex. Please show all the mathematical
derivations that you perform.
- In class, we used a mysterious parameter
 to represent a
variable continuously increasing along a ray. There are other
variables that can play a similar role.
to represent a
variable continuously increasing along a ray. There are other
variables that can play a similar role.
- Transform the isotropic ray tracing system
into an equivalent system that uses  instead of
instead of
 , where
, where  represents the length of the ray trajectory:
represents the length of the ray trajectory:
Remember to check physical dimensions.
- Suppose you are given
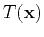 - the traveltime from
the source to all points
- the traveltime from
the source to all points  in the domain of
interest. Your task is to find
in the domain of
interest. Your task is to find
 - the length of
the ray trajectory at all
- the length of
the ray trajectory at all  . Derive a first-order partial
differential equation that connects
. Derive a first-order partial
differential equation that connects
 and
and  .
.
- The so-called ``parabolic'' or
 eikonal
equation (Bamberger et al., 1988; Claerbout, 1985; Tappert, 1977) has the form
eikonal
equation (Bamberger et al., 1988; Claerbout, 1985; Tappert, 1977) has the form
 |
(7) |
where
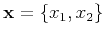 is a point in space,
is a point in space, 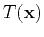 is the traveltime, and
is the traveltime, and  is slowness.
is slowness.
- Derive the ray tracing system for equation (7)
where  represents
represents
 and
and
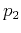 represents
represents
 .
.
- Assuming a constant slowness
 , solve
the ray tracing system for a point source at the origin
, solve
the ray tracing system for a point source at the origin
 .
.
- Using the ray tracing solution, find the shape of the
wavefronts defined by equation (7) in the case of a
constant slowness.
- The isotropic eikonal equation
 |
(12) |
describes wavefronts of the wave equation
 |
(13) |
with omitted possible first- and zero-order terms.
What wave equation corresponds to equation (7)?
 |
(14) |
Next: Computational part
Up: Homework 1
Previous: Prerequisites
2019-09-05