Inverse B-spline interpolation

Beyond B-splines

It is not too difficult to construct a convolutional basis with better interpolation properties than those of B-splines, for example by sacrificing their smoothness. The following piece-wise cubic function has a lower smoothness than $\beta ^3(x)$ in equation (13) but slightly better interpolation behavior:

$$\mu^3(x) = \left\{\begin{array}{lcr} \displaystyle \left(... ...t x\vert \geq 1 \\ 0, & \mbox{elsewhere} & \end{array}\right.$$ (14)

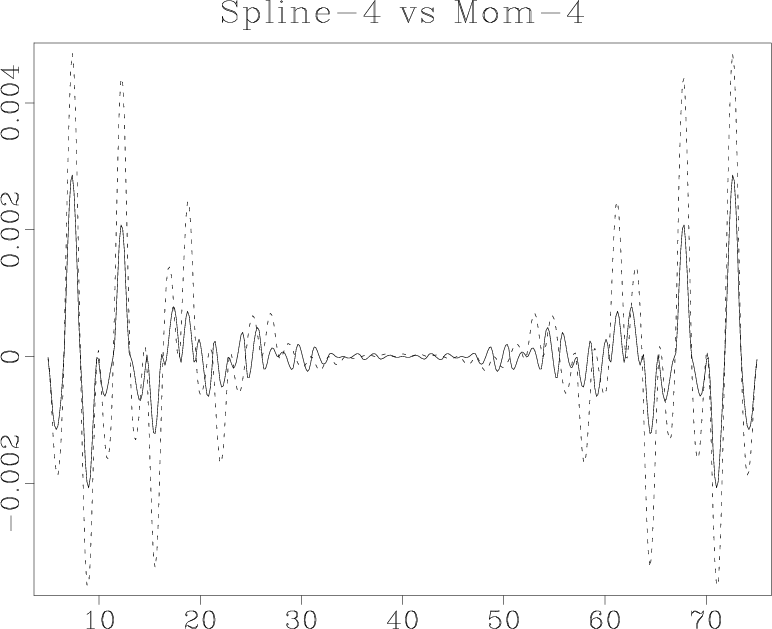
Figures 23 and 24 compare the test interpolation errors and discrete responses of methods based on the B-spline function $\beta ^3(x)$ and the lower smoothness function $\mu^3(x)$. The latter method has a slight but visible performance advantage and a slightly wider discrete spectrum.

spl4mom4 Figure 23. Interpolation error of the third-order B-spline interpolant (dashed line) compared to that of the lower smoothness spline interpolant (solid line).

specspl4mom4 Figure 24. Discrete interpolation responses of third-order B-spline and lower smoothness spline interpolants (left) and their discrete spectra (right) for $x=0.7$.

Blu et al. (1998) have developed a general approach for constructing non-smooth piece-wise functions with optimal interpolation properties. However, the gain in accuracy is often negligible in practice. In the rest of this paper, I use the classic B-spline method.

Inverse B-spline interpolation