 |
 |
 |
 | Inverse B-spline interpolation |  |
![[pdf]](icons/pdf.png) |
Next: Spline regularization
Up: Fomel: Inverse interpolation
Previous: Seismic applications of forward
In the notation of Claerbout (1999), inverse interpolation amounts to a
least-squares solution of the system
where 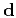 is a vector of known data
is a vector of known data 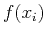 at irregular
locations
at irregular
locations 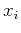 ,
, 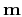 is a vector of unknown function values
is a vector of unknown function values
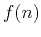 at a regular grid
at a regular grid 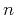 ,
, 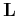 is a linear interpolation
operator of the general form (1),
is a linear interpolation
operator of the general form (1), 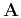 is an
appropriate regularization (model styling) operator, and
is an
appropriate regularization (model styling) operator, and 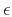 is
a scaling parameter. In the case of B-spline interpolation, the
forward interpolation operator
is
a scaling parameter. In the case of B-spline interpolation, the
forward interpolation operator 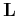 becomes a cascade of two
operators: recursive deconvolution
becomes a cascade of two
operators: recursive deconvolution
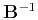 , which converts the
model vector
, which converts the
model vector 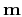 to the vector of spline coefficients
to the vector of spline coefficients
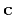 , and a spline basis construction operator
, and a spline basis construction operator 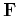 .
System (15-16) transforms to
.
System (15-16) transforms to
We can rewrite (17-18) in the form that
involves only spline coefficients:
After we find a solution of system (19-20),
the model 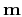 will be reconstructed by the simple convolution
will be reconstructed by the simple convolution
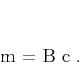 |
(21) |
This approach resembles a more general method of model preconditioning
(Fomel, 1997a).
The inconvenient part of system (19-20) is the
complex regularization operator 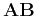 . Is it possible to avoid
the cascade of
. Is it possible to avoid
the cascade of 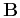 and
and 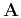 and to construct a
regularization operator directly applicable to the spline coefficients
and to construct a
regularization operator directly applicable to the spline coefficients
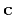 ? In the following subsection, I develop a method for
constructing spline regularization operators from differential
equations.
? In the following subsection, I develop a method for
constructing spline regularization operators from differential
equations.
Subsections
 |
 |
 |
 | Inverse B-spline interpolation |  |
![[pdf]](icons/pdf.png) |
Next: Spline regularization
Up: Fomel: Inverse interpolation
Previous: Seismic applications of forward
2014-02-15
![]() . Is it possible to avoid
the cascade of
. Is it possible to avoid
the cascade of ![]() and
and ![]() and to construct a
regularization operator directly applicable to the spline coefficients
and to construct a
regularization operator directly applicable to the spline coefficients
![]() ? In the following subsection, I develop a method for
constructing spline regularization operators from differential
equations.
? In the following subsection, I develop a method for
constructing spline regularization operators from differential
equations.