 |
 |
 |
 | Acoustic wavefield evolution as function of source location perturbation |  |
![[pdf]](icons/pdf.png) |
Next: The implementation
Up: Alkhalifah: Source perturbation wave
Previous: Theory
The Green's function represents the response and behavior of the wavefield if the source was a point impulse given theoretically by
the Dirac delta function. The function allows us to solve the wave equation using an integral formulation as we convolve the Green's function
with a source function. The most complicated part of this
type of solution of the wave equation is the construction of the Green's function. Kirchhoff modeling and migration is a special case of this type of integral
solution and provides incredible speed upgrades over finite difference implementations with some loss in quality, because of the limitations
in the calculation of the phase and amplitude components of the Green's function.
Since Green's function for the wave equation satisfies the following formula:
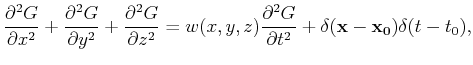 |
|
|
(9) |
where 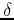 is the Dirac delta function, with
is the Dirac delta function, with 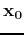 (
(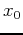 ,
, 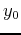 ,
, 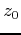 ), and
), and 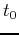 is the possible location and time of the source pulse, respectively.
The solution of equation (1) with a source function
is the possible location and time of the source pulse, respectively.
The solution of equation (1) with a source function
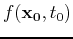 is given by
is given by
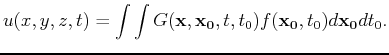 |
|
|
(10) |
In typical imaging applications, the Green's function is evaluated upfront and stored in tables for use in prestack modeling and migration.
For source perturbations, these stored Green's functions can be used to approximate the wavefield for a shift in the source location
by using a source function that is based on Taylor's series expansion, without the need to modify the Green's function. Specifically, considering that in the
first-order perturbation
equation (4):
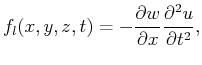 |
|
|
(11) |
then since equation (4) has the same form as the wave equation with the same velocity function,
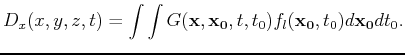 |
|
|
(12) |
The same argument holds for the second-order perturbation equation (7)
with a slightly more complicated source function given by
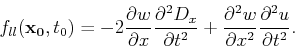 |
(13) |
Thus, the wavefield form can be approximated for a source perturbed
a distance 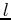 using
using
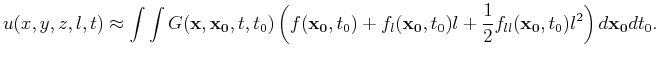 |
|
|
(14) |
Thus, the wavefield corresponding to a certain source location can be directly evaluated using the background Green's function with a modified source function, and these
modifications, unlike the conventional ones, are dependent on lateral velocity variations.
 |
 |
 |
 | Acoustic wavefield evolution as function of source location perturbation |  |
![[pdf]](icons/pdf.png) |
Next: The implementation
Up: Alkhalifah: Source perturbation wave
Previous: Theory
2013-04-02