|
|
|
|
A fast butterfly algorithm for generalized Radon transforms |
The coefficients
![]() for
for ![]() are however not readily available. The so-called butterfly algorithm turns out to be an appropriate tool. The butterfly algorithm was introduced by Michielssen and Boag (1996), and generalized by O'Neil et al. (2010) and Candès et al. (2009). Different applications include sparse Fourier transform (Ying, 2009), and radar imaging (Demanet et al., 2012). Demanet et al. (2012) also provide a complete error analysis of the method introduced by Candès et al. (2009).
are however not readily available. The so-called butterfly algorithm turns out to be an appropriate tool. The butterfly algorithm was introduced by Michielssen and Boag (1996), and generalized by O'Neil et al. (2010) and Candès et al. (2009). Different applications include sparse Fourier transform (Ying, 2009), and radar imaging (Demanet et al., 2012). Demanet et al. (2012) also provide a complete error analysis of the method introduced by Candès et al. (2009).
The idea of the butterfly algorithm is to obtain
![]() for
for ![]() at the last step of a hierarchical construction of all the coefficients
at the last step of a hierarchical construction of all the coefficients
![]() for all pairs of admissible boxes
for all pairs of admissible boxes ![]() belonging to a quad tree structure. The algorithm starts with very small boxes
belonging to a quad tree structure. The algorithm starts with very small boxes ![]() , where
, where
![]() are easily computed by direct summation, and gradually increases the sizes of the boxes
are easily computed by direct summation, and gradually increases the sizes of the boxes ![]() in a multiscale fashion. In tandem, the sizes of the boxes
in a multiscale fashion. In tandem, the sizes of the boxes ![]() where
where ![]() is evaluated must decrease to respect the admissibility of each couple
is evaluated must decrease to respect the admissibility of each couple ![]() . The computation then mostly consists in updating coefficients
. The computation then mostly consists in updating coefficients
![]() from one scale to the next -- from finer to coarser
from one scale to the next -- from finer to coarser ![]() boxes, and from coarser to finer
boxes, and from coarser to finer ![]() boxes.
boxes.
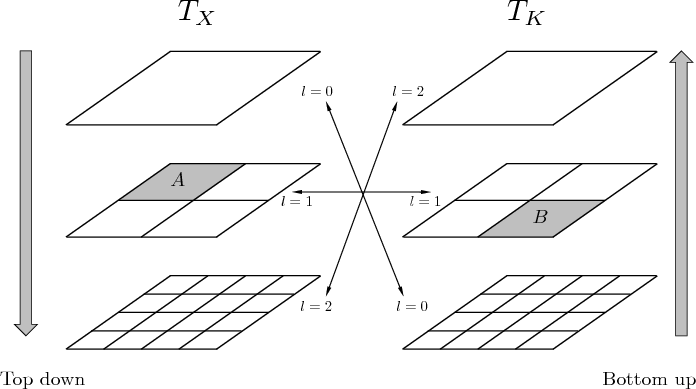
The main data structure underlying the algorithm is a pair of quad trees ![]() and
and ![]() . The tree
. The tree ![]() has
has
![]() as its root box (level 0
) and is built by recursive, dyadic partitioning until level
as its root box (level 0
) and is built by recursive, dyadic partitioning until level ![]() , where the finest boxes are of sidelength
, where the finest boxes are of sidelength ![]() . The tree
. The tree ![]() is built similarly but in the opposite direction. Figure 2 shows such a partition for
is built similarly but in the opposite direction. Figure 2 shows such a partition for ![]() . A crucial property of this structure is that at arbitrary level
. A crucial property of this structure is that at arbitrary level ![]() , the sidelengths of a box
, the sidelengths of a box ![]() in
in ![]() and a box
and a box ![]() in
in ![]() always satisfy
always satisfy
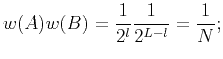 |
(22) |
|
|---|
|
tree
Figure 2. The butterfly quad tree structure for the special case of |
|
|
|
|
|
|
A fast butterfly algorithm for generalized Radon transforms |