|
|
|
|
De-aliased seismic data interpolation using seislet transform with low-frequency constraint |
Next: De-aliased interpolation by low-frequency Up: Methods Previous: Seislet transform
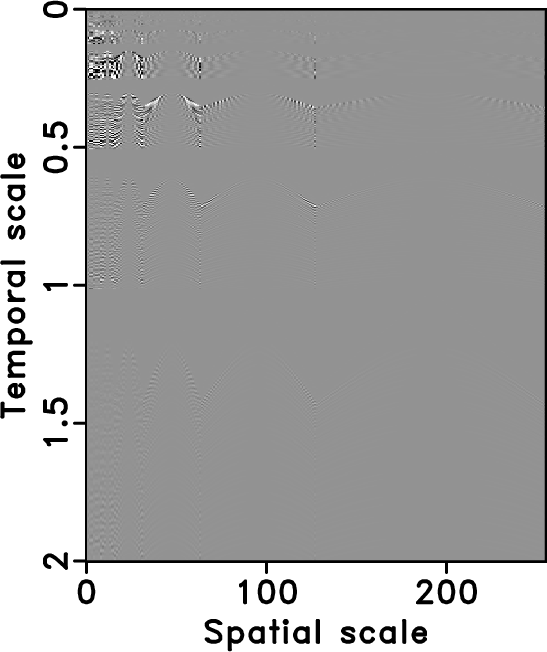
In order to effectively compare the sparseness of different transforms, we first select an input dataset (here, we use the synthetic example shown in Figure 3a as the input dataset). Then we transform the input data into sparse transform domain using different sparse transforms. Figure 1 shows different transformed domains for the input data. The 2-D Fourier transform in this case means the ![]() transform. The 2-D wavelet transform means implementing the 1-D wavelet transform along the temporal direction first and along the spatial direction second. The 2-D seislet transform means implementing the seislet transform along the spatial direction first and 1-D seislet transform along the temporal direction second. The 2-D curvelet transform refers to the 2-D wedge wrapping based fast discrete curvelet transform Candès et al. (2006). Next we sort the coefficients in the transform domains into decaying 1-D vectors according to the coefficient amplitude and scale the 1-D vectors. Finally we plot the decaying coefficients with respect to the sequence number for all the transforms in one plot. Figure 2 shows a comparison between the decay of sorted coefficients in the 2-D Fourier transform, 2-D wavelet transform, 2-D seislet transform and 2-D curvelet transform domains. Our experiments show that the seislet coefficients decay significantly faster than coefficients of the other transforms, which indicates a more compact structure of the seislet domain. Thus, our POCS based interpolation approach is preferred to use the 2-D seislet transform domain as the sparsity-promoting transform. Although the sparsity comparison is based on the well-sampled data, the same conclusion can be extended to the under-sampled case. It is worth to be mentioned that most sparse transforms (in their original form) including the four mentioned transforms can not obtain acceptable reconstruction results for under-sampled data with regularly missing traces.
transform. The 2-D wavelet transform means implementing the 1-D wavelet transform along the temporal direction first and along the spatial direction second. The 2-D seislet transform means implementing the seislet transform along the spatial direction first and 1-D seislet transform along the temporal direction second. The 2-D curvelet transform refers to the 2-D wedge wrapping based fast discrete curvelet transform Candès et al. (2006). Next we sort the coefficients in the transform domains into decaying 1-D vectors according to the coefficient amplitude and scale the 1-D vectors. Finally we plot the decaying coefficients with respect to the sequence number for all the transforms in one plot. Figure 2 shows a comparison between the decay of sorted coefficients in the 2-D Fourier transform, 2-D wavelet transform, 2-D seislet transform and 2-D curvelet transform domains. Our experiments show that the seislet coefficients decay significantly faster than coefficients of the other transforms, which indicates a more compact structure of the seislet domain. Thus, our POCS based interpolation approach is preferred to use the 2-D seislet transform domain as the sparsity-promoting transform. Although the sparsity comparison is based on the well-sampled data, the same conclusion can be extended to the under-sampled case. It is worth to be mentioned that most sparse transforms (in their original form) including the four mentioned transforms can not obtain acceptable reconstruction results for under-sampled data with regularly missing traces.



|
|---|
|
hyper-fk,hyper-dwt,hyper-seiss,hyper-curv-img
Figure 1. Comparison among different sparsity-promoting transforms based on the synthetic example shown in Figure 3a. (a) 2-D Fourier transform domain. (b) 2-D Wavelet transform domain. (c) 2-D Seislet transform domain. (d) 2-D Curvelet transform domain. |
|
|

|
|---|
|
hyper-c
Figure 2. Coefficients decaying diagram of different sparsity-promoting transforms. |
|
|