The principal problem of seismic data reconstruction is to solve the underdetermined inversion problem:
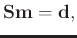 |
(1) |
where
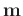 is the well-sampled seismic data (or model),
is the well-sampled seismic data (or model),
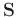 denotes the sampling operator, and
denotes the sampling operator, and
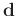 denotes the observed data Chen et al. (2014a). Because of the missing traces, the operator
denotes the observed data Chen et al. (2014a). Because of the missing traces, the operator
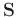 is highly singular and thus makes equation 1 highly underdetermined.
is highly singular and thus makes equation 1 highly underdetermined.
There have been many different algorithms for solving equation 1 by imposing different constraints. In the seismic data processing field, the POCS algorithm Abma and Kabir (2006) is one of the most widely used methods to interpolate seismic data with irregularly missing traces, and has the following iterative expression:
![$\displaystyle \mathbf{m}_{n+1}=\mathbf{d}+(\mathbf{I}-\mathbf{S})\mathbf{A}^{-1}\mathbf{T}\mathbf{A}[\mathbf{m}_n],$](img16.png) |
(2) |
where
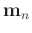 denotes the reconstructed data after
denotes the reconstructed data after 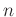 th iteration,
th iteration,
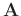 and
and
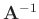 are the forward and inverse sparsity-promoting transforms,
are the forward and inverse sparsity-promoting transforms,
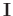 is an identity matrix and
is an identity matrix and
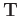 is a thresholding operator. However, for regularly missing traces, POCS can not obtain satisfied results because of the strong aliasing noise in the sparse domain. Gan et al. (2015) has shown that the seislet-based POCS algorithm can still be effective for interpolating regularly missing traces provided that an accurate local slope map can be obtained. All the examples in this paper are based on the iterative framework 2. The thresholding operator
is a thresholding operator. However, for regularly missing traces, POCS can not obtain satisfied results because of the strong aliasing noise in the sparse domain. Gan et al. (2015) has shown that the seislet-based POCS algorithm can still be effective for interpolating regularly missing traces provided that an accurate local slope map can be obtained. All the examples in this paper are based on the iterative framework 2. The thresholding operator
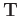 is chosen as a soft-thresholding operator in the seislet domain:
is chosen as a soft-thresholding operator in the seislet domain:
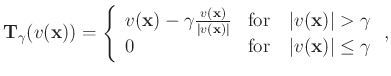 |
(3) |
where
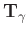 corresponds to the soft thresholding operator with a threshold value
corresponds to the soft thresholding operator with a threshold value 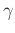 .
.
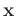 denotes the coordinates vector.
denotes the coordinates vector.
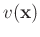 denotes the value the spatial point
denotes the value the spatial point
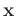 .
.
2020-02-28