Appendix A: Review of EMD based dip filter

The empirical mode decomposition (EMD) based dip filter is implemented in 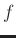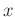$f$-$x$ domain. As EMD (Chen et al., 2015; Huang et al., 1998; Gan et al., 2015b) can empirically decompose a 1 D signal into different components that corresponds to different oscillating frequency, one can apply EMD to each frequency slice in 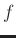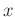$f$-$x$ domain and gather the same oscillating components for each frequency slice for separated 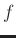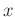$f$-$x$ domain profile. One then can get different separated seismic sections by transforming the separated 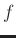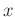$f$-$x$ data back to 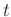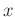$t$-$x$ domain. As the different oscillating components in each frequency slice of 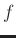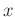$f$-$x$ domain correspond to different dip components, the separating process acts as an adaptive dip filter.

The formulation of the EMD based dip filter was given by Chen and Ma (2014):

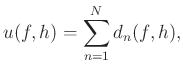$$u(f,h)=\sum_{n=1}^{N}d_n(f,h),$$ (14)

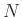where $N$ is the number of dip components or the number of EMD decomposed components. 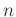$n$ denotes index, 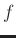$f$ denotes frequency, and 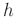$h$ denotes spatial trace index. The decomposition is done in each frequency slice in the frequency-space domain via EMD. The details of EMD can be found in Huang et al. (1998).

Equation 14 is formulated in the frequency domain in its original form. In the time-space domain, the EMD based dip filtering is simply

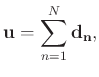$$\mathbf{u}=\sum_{n=1}^{N}\mathbf{d_n},$$ (15)

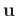where $\mathbf{u}$ is the vectorized seismic data, 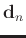$\mathbf{d}_n$ is the 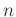$n$th dip component after using the EMD based dip filter. It is obvious that the EMD based dip filter is a linear transform and the summation of all the dip components is the original seismic image.