Because equation 7 is a singular value decomposition (SVD) of the signal matrix
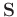 , the left matrix in equation 7 is a unitary matrix:
, the left matrix in equation 7 is a unitary matrix:
![$\displaystyle \mathbf{I}=\mathbf{U}^S(\mathbf{U}^S)^H=[\mathbf{U}_1^S\quad \mat...
...[\begin{array}{c}
(\mathbf{U}_1^S)^H \\
(\mathbf{U}_2^S)^H
\end{array}\right].$](img118.png) |
(21) |
Combining equations 4, 8, and 21, we can derive:
![\begin{displaymath}\begin{split}
\mathbf{M}&=\mathbf{S}+\mathbf{N} \\
&=\mathbf...
...}(\mathbf{N}^H\mathbf{U}_2^S)^H
\end{array}\right],
\end{split}\end{displaymath}](img119.png) |
(22) |
where 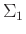 and
and 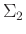 are introduced matrices and are diagonal and positive definite.
are introduced matrices and are diagonal and positive definite.
In order to make the right matrix orthonormal, we make two assumptions:
- The noise is close to white noise in the sense that
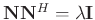 .
.
- The signal is orthogonal to the noise in the sense that
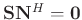 .
.
We let
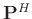 denote the right matrix of the last equation in 22, then
denote the right matrix of the last equation in 22, then
![\begin{displaymath}\begin{split}
&\mathbf{P}^H\mathbf{P} \\
&=\left[\begin{arra...
...{11} & p_{12}\\
p_{21} & p_{22}
\end{array}\right]
\end{split}\end{displaymath}](img123.png) |
(23) |
where
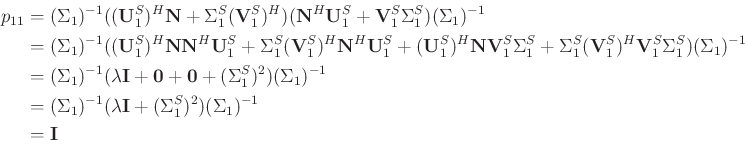 |
(24) |
when
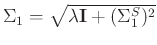 .
.
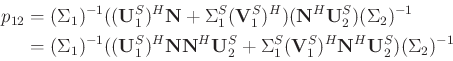 |
(25) |
Since
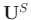 is an orthogonal matrix, then
is an orthogonal matrix, then
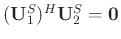 . Since
. Since
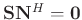 , then
, then
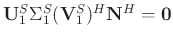 , thus
, thus
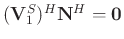 . In the same way, since
. In the same way, since
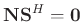 , thus
, thus
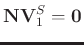 .
Then,
.
Then,
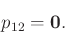 |
(26) |
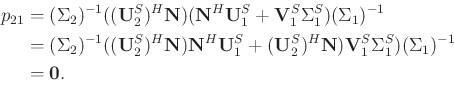 |
(27) |
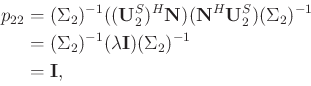 |
(28) |
when
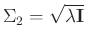 .
Thus, we prove that
.
Thus, we prove that
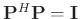 when
when 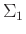 and
and 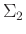 are appropriately chosen, and
are appropriately chosen, and
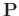 is orthonormal.
is orthonormal.
2020-02-21
![]() denote the right matrix of the last equation in 22, then
denote the right matrix of the last equation in 22, then