 |
 |
 |
 | Kirchhoff migration using eikonal-based computation of traveltime source-derivatives |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Li & Fomel: Kirchhoff
Previous: Conclusion
We thank the editors, Samuel Gray, and three anonymous reviewers for constructive
suggestions that helped improving the quality of the manuscript. We thank Tariq Alkhalifah and
Alexander Vladimirsky for useful discussions and sponsors of the Texas Consortium for Computational
Seismology (TCCS) for financial support of this research. This publication is authorized by
the Director, Bureau of Economic Geology, The University of Texas at Austin.
Appendix
A
FMM implementation of source-derivatives
The FMM is a non-iterative eikonal solver with 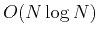 complexity,
where
complexity,
where 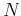 is the total number of grid points of the discretized domain.
It relies on a heap data structure to keep the updating sequence, and
a local one-sided upwind finite-difference scheme for ensuring the
causality (Sethian, 1996). Consider in 3D a cubic domain discretized into Cartesian grids,
with uniform grid size of
is the total number of grid points of the discretized domain.
It relies on a heap data structure to keep the updating sequence, and
a local one-sided upwind finite-difference scheme for ensuring the
causality (Sethian, 1996). Consider in 3D a cubic domain discretized into Cartesian grids,
with uniform grid size of
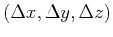 . Let
. Let
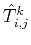 be the traveltime value at vertices
be the traveltime value at vertices
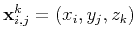 and define difference operator
and define difference operator 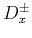 for
for  direction as
direction as
 |
(14) |
The causality condition requires picking an upwind neighbor in all
directions at
 .
.
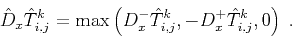 |
(15) |
After similar definitions for 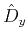 and
and  , the local
upwind scheme in FMM for equation 3 reads
, the local
upwind scheme in FMM for equation 3 reads
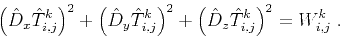 |
(16) |
For
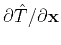 in equation 6
and
in equation 6
and
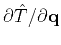 in equation 5,
we can apply the same upwind strategy:
in equation 5,
we can apply the same upwind strategy:
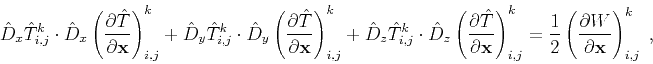 |
(17) |
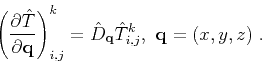 |
(18) |
where in equation A-4 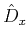 ,
, 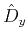 and
and  are chosen according to
are chosen according to
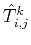 , regardless of
, regardless of
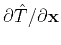 . Finally,
. Finally,
 |
(19) |
To incorporate the computation of traveltime source-derivatives into
FMM, one only needs to add equations A-4, A-5 and
A-6 after A-3. An extra upwind sorting and
solving after pre-computing 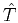 is not necessary. The total complexity of
FMM with the auxiliary output of traveltime source-derivative remains
is not necessary. The total complexity of
FMM with the auxiliary output of traveltime source-derivative remains 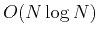 .
.
Appendix
B
Interpolation of source-derivatives
Applying the chain-rule 13 to equation 10, we arrive at the interpolation
equation for source-derivatives in the cubic Hermite scheme:
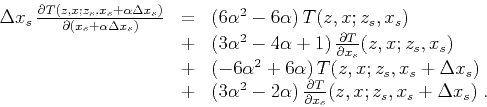 |
(20) |
Analogously, the interpolation of source-derivatives in the linear scheme 11 reads:
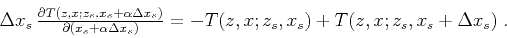 |
(21) |
which is a simple first-order finite-difference estimation. Finally, in the case of shift scheme
12, the partial derivative
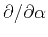 must be applied to the shifted
traveltime terms at the same time:
must be applied to the shifted
traveltime terms at the same time:
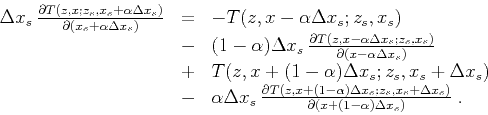 |
(22) |
The required spatial derivatives can be estimated from the traveltime table by means of
finite-differences, for example by using the upwind approximation A-2.
 |
 |
 |
 | Kirchhoff migration using eikonal-based computation of traveltime source-derivatives |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Li & Fomel: Kirchhoff
Previous: Conclusion
2013-07-26
![]() complexity,
where
complexity,
where ![]() is the total number of grid points of the discretized domain.
It relies on a heap data structure to keep the updating sequence, and
a local one-sided upwind finite-difference scheme for ensuring the
causality (Sethian, 1996). Consider in 3D a cubic domain discretized into Cartesian grids,
with uniform grid size of
is the total number of grid points of the discretized domain.
It relies on a heap data structure to keep the updating sequence, and
a local one-sided upwind finite-difference scheme for ensuring the
causality (Sethian, 1996). Consider in 3D a cubic domain discretized into Cartesian grids,
with uniform grid size of
![]() . Let
. Let
![]() be the traveltime value at vertices
be the traveltime value at vertices
![]() and define difference operator
and define difference operator ![]() for
for ![]() direction as
direction as