|
|
|
|
A parallel sweeping preconditioner for heterogeneous 3D Helmholtz equations |
|
|---|
|
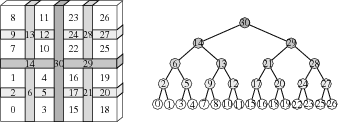
sep-tree
Figure 3. A separator-based supernodal elimination tree (right) over a quasi-2D subdomain (left). |
|
|
|
|---|
|
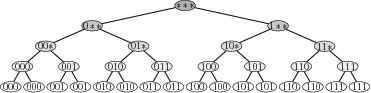
subteam
Figure 4. Overlay of the process ranks (in binary) of the owning subteams of each supernode from the elimination tree in Fig. 3 when the tree is assigned to eight processes using a subtree-to-subteam mapping; a `*' is used to denote both 0 and 1, so that ` |
|
|
Roughly speaking, the analysis in (26) shows that,
if ![]() processes are used in the multifrontal factorization of our quasi-2D
subdomain problems, then we must have
processes are used in the multifrontal factorization of our quasi-2D
subdomain problems, then we must have
![]() in order to
maintain constant efficiency as
in order to
maintain constant efficiency as ![]() is increased; similarly, if
is increased; similarly, if ![]() processes are used in the multifrontal triangular solves for a subdomain,
then we must have
processes are used in the multifrontal triangular solves for a subdomain,
then we must have
![]() (where we use
(where we use ![]() to denote that the equality holds within logarithmic
factors).
Since we can simultaneously factor the
to denote that the equality holds within logarithmic
factors).
Since we can simultaneously factor the
![]() subdomain
matrices, we denote the total number of processes as
subdomain
matrices, we denote the total number of processes as ![]() and set
and set
![]() and
and
![]() ; then the subdomain factorizations only require
that
; then the subdomain factorizations only require
that
![]() , while the subdomain solves have the
much stronger constraint that
, while the subdomain solves have the
much stronger constraint that
![]() .
This last constraint should be considered unacceptable, as we have the
conflicting requirement that
.
This last constraint should be considered unacceptable, as we have the
conflicting requirement that
![]() in
order to store the factorizations in memory. It is therefore advantageous to
consider more scalable alternatives to standard multifrontal triangular solves,
even if they require additional computation.
in
order to store the factorizations in memory. It is therefore advantageous to
consider more scalable alternatives to standard multifrontal triangular solves,
even if they require additional computation.
|
|
|
|
A parallel sweeping preconditioner for heterogeneous 3D Helmholtz equations |