|
|
|
|
Multi-channel quality factor Q estimation |
Next: Discussions Up: Chen, 2019: Multi-channel Q Previous: Spectral division by shaping
The first synthetic example is shown in Figure 1. We apply band-limited random noise to the clean data to simulate a realistic data that contains random ambient noise, as shown in Figure 1a. The signal-to-noise ratio (SNR) of the noisy data is -4.5 dB. We use the following SNR definition (Mousavi and Langston, 2017; Mousavi et al., 2016; Mousavi and Langston, 2016; Chen et al., 2016; Chen, 2017):
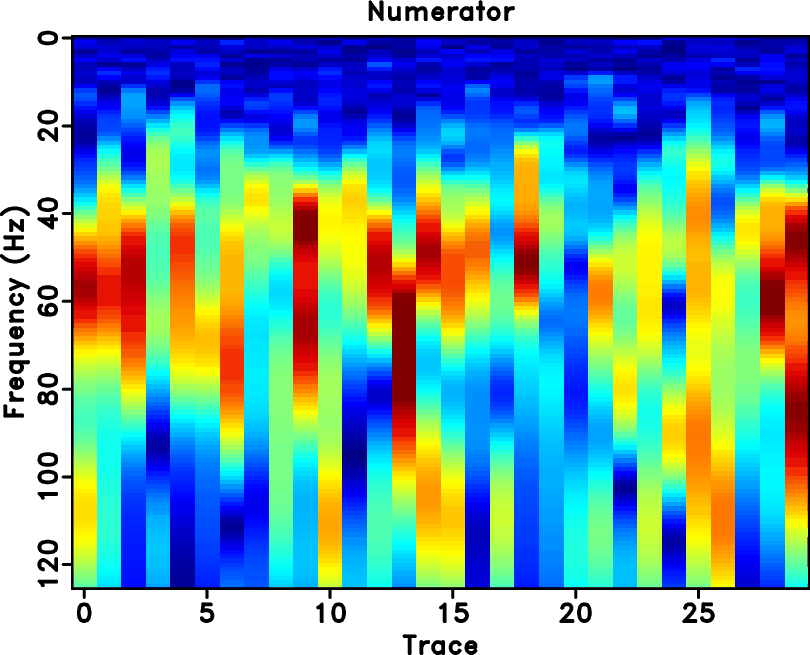
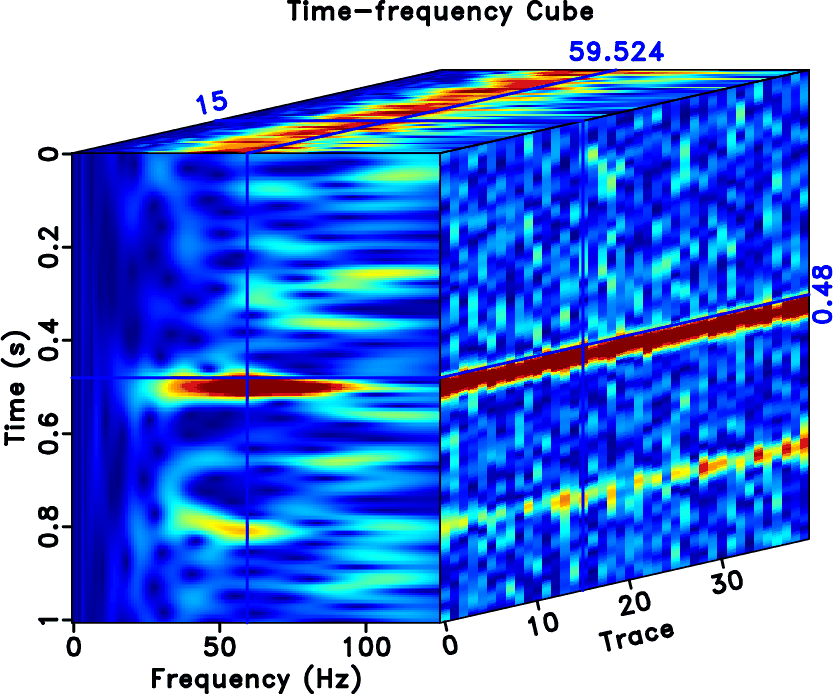
The random noise is very strong and the the useful reflection signals are almost buried in the strong noise. Figure 1b shows a single trace (the middle trace) that is extracted from the multi-channel seismic section. To apply the spectral ratio method (SRM), we first transform the seismic data from time-space domain to time-frequency-space domain using the S transform. We show the time-frequency cube of the seismic data in Figure 2. Because of the strong random noise, the 2D time-frequency analysis becomes highly affected and resulted time-frequency map is highly irregular, as revealed by the front panel in Figure 2. However, when time-frequency maps are arranged section by section in a 3D cube, the peaks (high amplitude anomaly) on the time-frequency maps become continuous along the space direction in the time-frequency cube. Thus, by taking the 3D time-frequency cube into consideration when computing the spectral ratio, the spatial coherence can be well utilized. Figure 3 shows two multi-channel time slice. Figure 3a shows the time slice corresponding to time ![]() and Figure 3b shows the time slice of
and Figure 3b shows the time slice of ![]() . The 2D matrix in Figure 3a is equivalent to the numerator
. The 2D matrix in Figure 3a is equivalent to the numerator
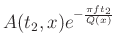 in equation 8 while the 2D matrix in Figure 3b corresponds to the denominator
in equation 8 while the 2D matrix in Figure 3b corresponds to the denominator
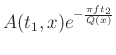 . In a vector form, Figure 3a corresponds to vector
. In a vector form, Figure 3a corresponds to vector
![]() in equation 9 and Figure 3b denotes the vector
in equation 9 and Figure 3b denotes the vector
![]() that constructs the diagonal matrix
that constructs the diagonal matrix
![]() in equation 9.
in equation 9.
The calculated the spectral ratio is shown in Figure 4a. Because of the two-dimensional smoothness contraint, the calculated spectral ratio is smooth on both axes and is not affected seriously by the random noise in the raw data. Figure 4b shows the predicted spectral ratio using the least-squares line-fitting. Figure 5a shows the calculated slope (![]() in equation 4) of the fitted line. Figure 5b shows the comparison of the estimated Q using single-channel and multi-channel methods, respectively. The blue line shows the exact Q that is used to generate the synthetic example. The red line shows the estimated Q using the proposed multi-channel Q estimation method. The pink line shows the estimated Q using the single-channel Q estimation method. The exact Q used for simulating the example is 60 and the estimated Q is very close to the exact Q and is almost spatially constant. However, due to the strong noise, the single-channel method obtains very unstable Q results, which are obviously not acceptable. In this example, we use a 5-point radius for the frequency direction smoothing and a 10-point radius for the space direction smoothing to obtain the result. We use the frequency range
in equation 4) of the fitted line. Figure 5b shows the comparison of the estimated Q using single-channel and multi-channel methods, respectively. The blue line shows the exact Q that is used to generate the synthetic example. The red line shows the estimated Q using the proposed multi-channel Q estimation method. The pink line shows the estimated Q using the single-channel Q estimation method. The exact Q used for simulating the example is 60 and the estimated Q is very close to the exact Q and is almost spatially constant. However, due to the strong noise, the single-channel method obtains very unstable Q results, which are obviously not acceptable. In this example, we use a 5-point radius for the frequency direction smoothing and a 10-point radius for the space direction smoothing to obtain the result. We use the frequency range
![]() Hz
Hz![]() Hz
Hz![]() for the least-squares line-fitting.
for the least-squares line-fitting.
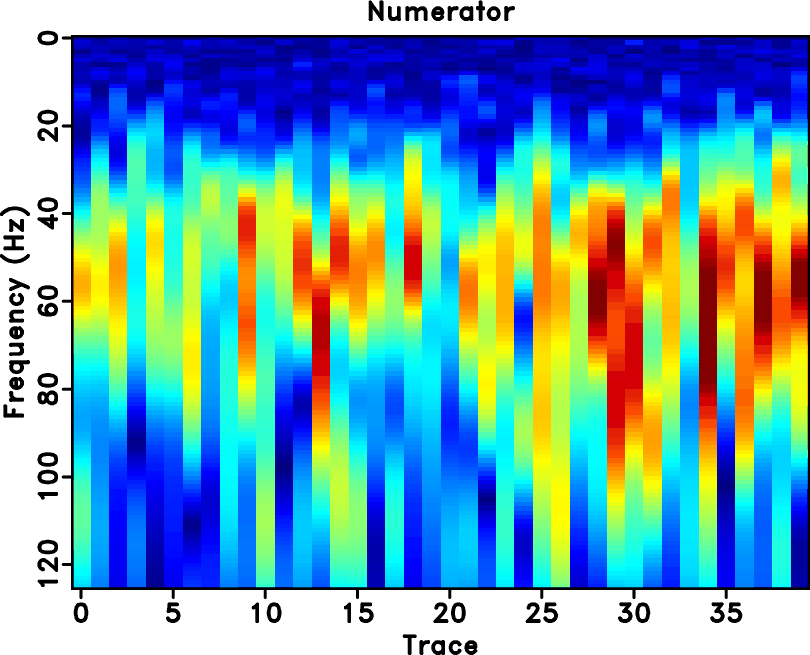
The second example with spatially varying Q is shown in Figure ![]() . Figure 6a shows the multi-channel seismic section. Figure 6b shows a single trace extracted from the seismic section. In this example, the quality factor, Q, varies from 40 to 80 from left to right. The SNR of this example is -1.53 dB. The time-frequency cube using the S transform is shown in Figure 7. Figure 8 shows the two constant time slices. Figure 8a and 8b correspond to
. Figure 6a shows the multi-channel seismic section. Figure 6b shows a single trace extracted from the seismic section. In this example, the quality factor, Q, varies from 40 to 80 from left to right. The SNR of this example is -1.53 dB. The time-frequency cube using the S transform is shown in Figure 7. Figure 8 shows the two constant time slices. Figure 8a and 8b correspond to ![]() s and
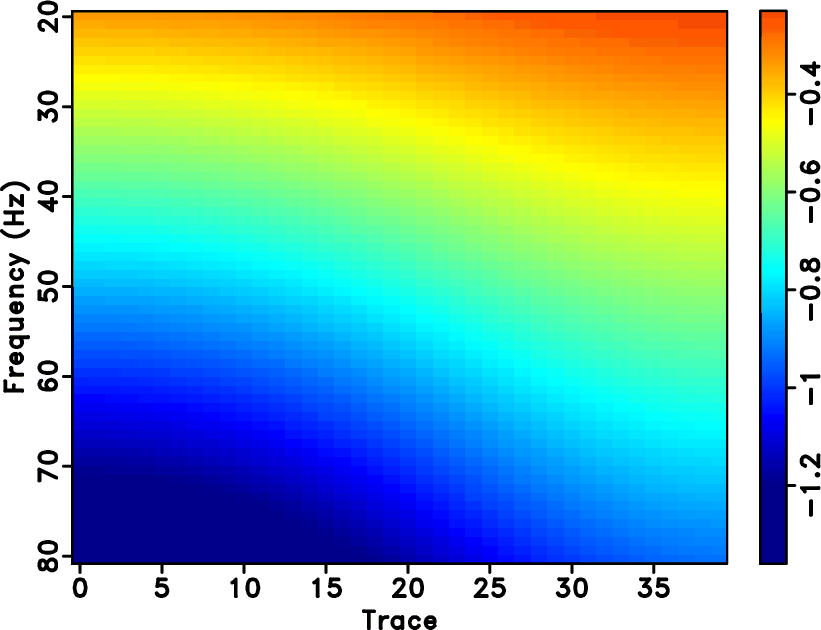
s and ![]() s, respectively. Figure 9a displays the spectral ratio result using the proposed shaping regularization method, which is smooth along both frequency and space directions. Figure 9b shows the predicted spectral ratio using the least-squares line-fitting method. It is clear that the smoothness regularized spectral ratio is close to the predicted spectral ratio by least-squares line-fitting. Figure 10 shows a comparison of different estimated Q results. The pink line from the single-channel Q estimation is highly oscillating, while the estimated space-varying Q curve as denoted by the red line is very close to the exact Q curve denoted by the blue line. In this example, we use a 5-point radius for the frequency direction smoothing and a 15-point radius for the space direction smoothing to obtain the result. We use the frequency range
s, respectively. Figure 9a displays the spectral ratio result using the proposed shaping regularization method, which is smooth along both frequency and space directions. Figure 9b shows the predicted spectral ratio using the least-squares line-fitting method. It is clear that the smoothness regularized spectral ratio is close to the predicted spectral ratio by least-squares line-fitting. Figure 10 shows a comparison of different estimated Q results. The pink line from the single-channel Q estimation is highly oscillating, while the estimated space-varying Q curve as denoted by the red line is very close to the exact Q curve denoted by the blue line. In this example, we use a 5-point radius for the frequency direction smoothing and a 15-point radius for the space direction smoothing to obtain the result. We use the frequency range
![]() Hz
Hz![]() Hz
Hz![]() for the least-squares line-fitting.
for the least-squares line-fitting.
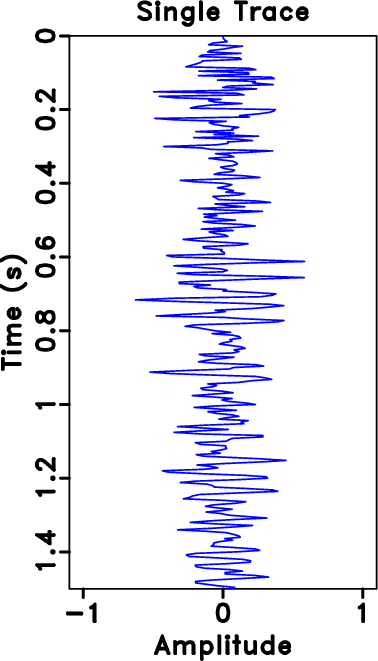
We then apply the proposed method to a real seismic data. The seismic section is shown in Figure 11a. It is clear that the field data is very noisy, not only containing strong random noise, but also corrupted by strong high-frequency linear noise. The highlighted area by the blue dashed lines and the frame box correspond to a hydrocarbon reservoir. We focus on studying the spatial variation of the quality factor in the reservoir area, which can provide insight on the viscosity and fluid property in this area. Figure 11b shows a single trace (first trace in the gather). Because of the strong noise and poor SNR of this dataset, it is difficult to distinguish between the reflections signals and noise in purely from the single trace.
Figure 12 shows the time-frequency cube of this example using the S transform. It is salient that the time-frequency maps help reveal the seismic events more clearly than the original amplitude profile. Figure 13 shows the two time-slices used for calculating the space-varying spectral ratio. Figure 13a corresponds to ![]() s and Figure 13b corresponds to
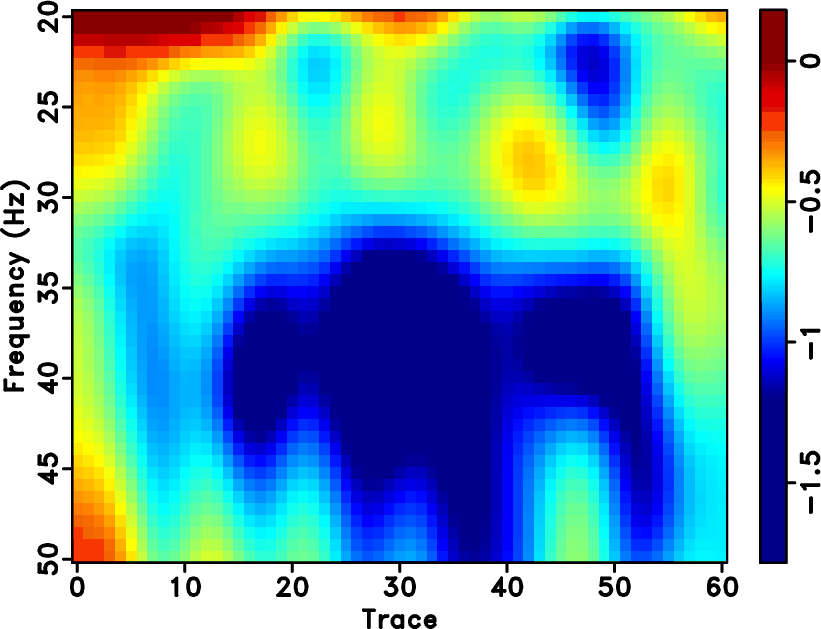
s and Figure 13b corresponds to ![]() s. Figure 14a shows the spectral ratio using the proposed method. Figure 14b shows the predicted spectral ratio by least-squares line-fitting. Figure 15 shows the comparison of estimated space-varying Q using the single-channel method and the proposed multi-channel method. The red line corresponds to the single-channel method, which is highly unstable while the blue line corresponds the multi-channel method, which is much smoother. In this example, we use a 5-point radius for the frequency direction smoothing and a 10-point radius for the space direction smoothing to obtain the result. To alleviate the influence of high-frequency noise, we use a relatively narrower frequency range
s. Figure 14a shows the spectral ratio using the proposed method. Figure 14b shows the predicted spectral ratio by least-squares line-fitting. Figure 15 shows the comparison of estimated space-varying Q using the single-channel method and the proposed multi-channel method. The red line corresponds to the single-channel method, which is highly unstable while the blue line corresponds the multi-channel method, which is much smoother. In this example, we use a 5-point radius for the frequency direction smoothing and a 10-point radius for the space direction smoothing to obtain the result. To alleviate the influence of high-frequency noise, we use a relatively narrower frequency range
![]() Hz
Hz![]() Hz
Hz![]() for the least-squares line-fitting.
for the least-squares line-fitting.


|
|---|
|
traces,trace-15
Figure 1. The synthetic example. (a) The multi-channel seismic section with SNR |
|
|

|
|---|
|
trace-st-N
Figure 2. Time-frequency cube of the multi-channel seismic section. Note that although the time-frequency map of a single-trace is irregular, the time-frequency map along the position direction is coherent. |
|
|

|
|---|
|
trace-f-t2-N,trace-f-t1-N
Figure 3. The multi-channel time slice of time |
|
|


|
|---|
|
trace-ratio-N,trace-lsfits
Figure 4. (a) The calculated spectral division. (b) The predicted spectral ratio via line fitting. |
|
|


|
|---|
|
trace-coef-N,trace-comp
Figure 5. (a) The slope ( |
|
|


|
|---|
|
linears,linear-15
Figure 6. The synthetic data example with spatially varying quality factor. (a) The multi-channel seismic profile with SNR |
|
|
|
|---|
|
linear-st-N
Figure 7. Time-frequency cube of the synthetic example with spatially varying quality factor. Note that the time-frequency map along the position direction is coherent. |
|
|

|
|---|
|
linear-f-t2-N,linear-f-t1-N
Figure 8. The multi-channel time slice of time |
|
|

|
|---|
|
linear-ratio-N,linear-lsfits
Figure 9. Synthetic data example with spatially varying quality factor. (a) The calculated spectral division. (b) The predicted spectral ratio via line fitting. |
|
|

|
|---|
|
linear-comp
Figure 10. The estimated Q using the proposed multi-channel method compared with the single-channel method and the exact solution for the synthetic example with spatially varying quality factor. The blue line corresponds to the exact Q that is used to generate the synthetic data. The pink line denotes the estimated result using the single-channel method. The red line denotes the estimated Q using the proposed multi-channel method. Note that the estimated Q using the proposed method is very close to the exact solution while the Q estimated from the single-channel method is highly unstable. |
|
|

|
|---|
|
field-0,field-single
Figure 11. The field data example. (a) The field seismic profile. (b) The first trace in (a). |
|
|

|
|---|
|
field-st-N
Figure 12. Time-frequency cube of the field seismic profile. Note that the time-frequency map along the position direction is coherent. |
|
|


|
|---|
|
field-f-t2-N,field-f-t1-N
Figure 13. The multi-channel time slice of time |
|
|

|
|---|
|
field-ratio-N,field-lsfits
Figure 14. Field data example. (a) The calculated spectral division. (b) The predicted spectral ratio via line fitting. |
|
|

|
|---|
|
field-comp
Figure 15. The estimated Q using the proposed multi-channel method compared with the single-channel method. The pink line denotes the estimated result using the single-channel method. The red line denotes the estimated Q using the proposed multi-channel method. Note that the estimated Q using the proposed method is spatially smooth while the Q estimated from the single-channel method is highly oscillating. |
|
|