The viscoacoustic wave equation with DFLs was first proposed by Zhu and Harris (2014) to characterize frequency-dependent attenuation and dispersion separately, which can be written as
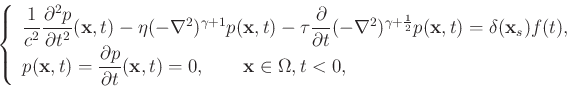 |
(1) |
where 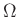 is a bounded domain in
is a bounded domain in 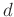 -dimensional space
-dimensional space
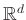 ,
,
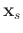 denotes the source position, and
denotes the source position, and 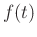 is the point source signature enforced at
is the point source signature enforced at
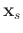 . The dimensionless parameter
. The dimensionless parameter
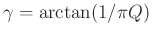 ranges within
ranges within 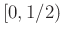 , and
, and
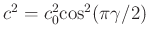 , where
, where 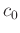 is the velocity model defined at the reference frequency
is the velocity model defined at the reference frequency 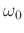 . The proportionality coefficients of two fractional Laplacians, separately representing dispersion and absorption, are given by
. The proportionality coefficients of two fractional Laplacians, separately representing dispersion and absorption, are given by
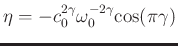 and
and
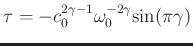 . Equation 1 seems to be attractive for
. Equation 1 seems to be attractive for 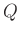 -RTM owing to its flexibility for separately compensating amplitude loss and correcting phase distortion. Treeby et al. (2010) and Zhu et al. (2014) stated that attenuation compensation based on this equation can be achieved by reversing the absorption proportionality coefficient in sign but leaving the equivalent dispersion parameter unchanged. My latest work (in Chapters 4 and 5) has analytically proved that Green's function of equation 1 is exponentially decreasing, whereas reversing the absorption proportionality coefficient in sign signifies replacing the Green's function with a phase-conjugated Green's function that is exponentially increasing (Wang et al., 2017c,2018c).
-RTM owing to its flexibility for separately compensating amplitude loss and correcting phase distortion. Treeby et al. (2010) and Zhu et al. (2014) stated that attenuation compensation based on this equation can be achieved by reversing the absorption proportionality coefficient in sign but leaving the equivalent dispersion parameter unchanged. My latest work (in Chapters 4 and 5) has analytically proved that Green's function of equation 1 is exponentially decreasing, whereas reversing the absorption proportionality coefficient in sign signifies replacing the Green's function with a phase-conjugated Green's function that is exponentially increasing (Wang et al., 2017c,2018c).
The novel paradigm of 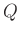 -RTM first proposed by Zhu et al. (2014), where the source wavefield
-RTM first proposed by Zhu et al. (2014), where the source wavefield
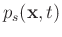 and receiver wavefield
and receiver wavefield
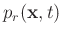 are compensated during forward extrapolation and time-reversal extrapolation simultaneously, coupled with a zero-lag crosscorrelation imaging condition, has proven to be a promising approach for generating high-resolution images and high-fidelity amplitude reflectors. Following the spirit of Treeby et al. (2010) and Zhu et al. (2014), the
are compensated during forward extrapolation and time-reversal extrapolation simultaneously, coupled with a zero-lag crosscorrelation imaging condition, has proven to be a promising approach for generating high-resolution images and high-fidelity amplitude reflectors. Following the spirit of Treeby et al. (2010) and Zhu et al. (2014), the 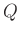 -compensated source wavefield
-compensated source wavefield
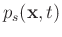 is the solution of the following equation:
is the solution of the following equation:
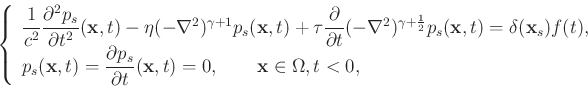 |
(2) |
and the 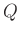 -compensated receiver wavefield
-compensated receiver wavefield
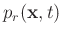 satisfies the following equation
satisfies the following equation
![\begin{displaymath}\left\{
\begin{array}{lr}
\dfrac{1}{c^2}\dfrac{\partial^2p_r}...
... \mathbf{x} \in \mathbf{x}_r, t \in [0,T], &
\end{array}\right.\end{displaymath}](img37.png) |
(3) |
where
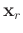 denotes the receiver positions,
denotes the receiver positions,
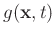 stands for the recorded seismic data at
stands for the recorded seismic data at
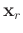 , which are reversed in time and enforced as the Dirichlet boundary condition. Finally, we realize
, which are reversed in time and enforced as the Dirichlet boundary condition. Finally, we realize 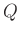 -RTM via the following zero-lag crosscorrelation imaging condition:
-RTM via the following zero-lag crosscorrelation imaging condition:
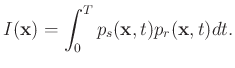 |
(4) |
However, an inevitable issue imposed by the crosscorrelation algorithm is that the forward wavefields need to be accessible at every time step (Anderson et al., 2012; Yang et al., 2016). Saving all forward wavefields requires tremendous memory and frequent disk I/O, which makes it impractical for large-scale 2D or 3D RTM (Symes, 2007; Tan and Huang, 2014), especially for CUDA-based RTM that demands data transfer between host and device (Yang et al., 2014).
2020-04-03
![]() -RTM first proposed by Zhu et al. (2014), where the source wavefield
-RTM first proposed by Zhu et al. (2014), where the source wavefield
![]() and receiver wavefield
and receiver wavefield
![]() are compensated during forward extrapolation and time-reversal extrapolation simultaneously, coupled with a zero-lag crosscorrelation imaging condition, has proven to be a promising approach for generating high-resolution images and high-fidelity amplitude reflectors. Following the spirit of Treeby et al. (2010) and Zhu et al. (2014), the
are compensated during forward extrapolation and time-reversal extrapolation simultaneously, coupled with a zero-lag crosscorrelation imaging condition, has proven to be a promising approach for generating high-resolution images and high-fidelity amplitude reflectors. Following the spirit of Treeby et al. (2010) and Zhu et al. (2014), the ![]() -compensated source wavefield
-compensated source wavefield
![]() is the solution of the following equation:
is the solution of the following equation: