Next: Data-push binning
Up: FAMILIAR OPERATORS
Previous: Adjoints of products are
In describing physical processes,
we often either specify models as values given on a uniform mesh
or we record data on a uniform mesh.
Typically we have
a function 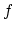 of time
of time 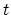 or depth
or depth 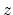 and we represent it by f(iz)
corresponding to
and we represent it by f(iz)
corresponding to 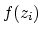 for
for
 where
where
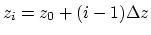 .
We sometimes need to handle depth as
an integer counting variable
.
We sometimes need to handle depth as
an integer counting variable 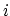 and we sometimes need to handle it as
a floating-point variable
and we sometimes need to handle it as
a floating-point variable 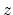 .
Conversion from the counting variable to the floating-point variable
is exact and is often seen in a computer idiom
such as either of
.
Conversion from the counting variable to the floating-point variable
is exact and is often seen in a computer idiom
such as either of
for (iz=0; iz < nz; iz++) { z = z0 + iz * dz;
for (i3=0; i3 < n3; i3++) { x3 = o3 + i3 * d3;
The reverse conversion from the floating-point variable
to the counting variable is inexact.
The easiest thing is to place it at the nearest neighbor.
This is done by solving for iz, then adding one half,
and then rounding down to the nearest integer.
The familiar computer idioms are:
iz = 0.5 + ( z - z0) / dz
i3 = 0.5 + (x3 - o3) / d3
A small warning is in order:
People generally use positive counting variables.
If you also include negative ones,
then to get the nearest integer,
you should do your rounding with the
C function floor.
Next: Data-push binning
Up: FAMILIAR OPERATORS
Previous: Adjoints of products are
2009-03-16