Next: Magic with 2-D Fourier
Up: SETTING UP 2-D FT
Previous: Signs in Fourier transforms
An example of a
two-dimensional Fourier transform
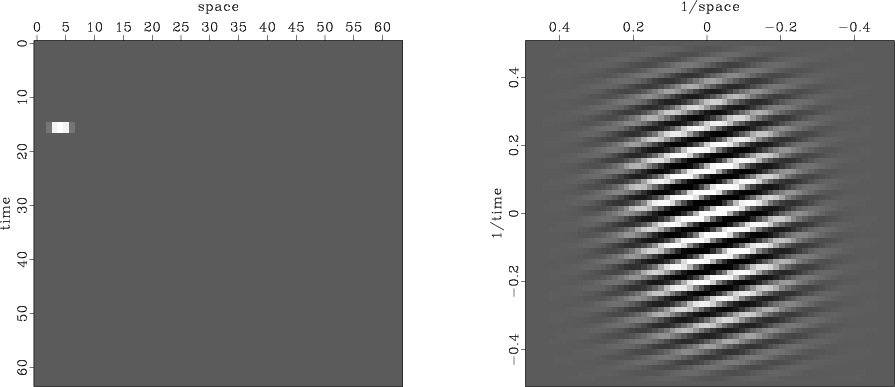
of a pulse is shown in Figure 5.
|
|---|
ft2dofpulse
Figure 5.
A broadened pulse (left) and the real part of its FT (right).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
Notice the location of the pulse.
It is closer to the time axis than the space axis.
This will affect the real part of the FT in a certain way
(see exercises).
Notice the broadening of the pulse.
It was an impulse smoothed over time (vertically) by convolution
with (1,1) and over space (horizontally) with (1,4,6,4,1).
This will affect the real part of the FT in another way.
Another example of a two-dimensional Fourier transform
is given in Figure 6.
This example simulates an impulsive air wave originating at a point
on the 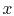 -axis.
We see a wave propagating in each direction
from the location of the source of the wave.
In Fourier space there are also two lines, one for each wave.
Notice that there are other lines which do not go through the origin;
these lines are called ``spatial aliases.''
Each actually goes through the origin
of another square plane that is not shown,
but which we can imagine alongside the one shown.
These other planes are periodic replicas of the one shown.
-axis.
We see a wave propagating in each direction
from the location of the source of the wave.
In Fourier space there are also two lines, one for each wave.
Notice that there are other lines which do not go through the origin;
these lines are called ``spatial aliases.''
Each actually goes through the origin
of another square plane that is not shown,
but which we can imagine alongside the one shown.
These other planes are periodic replicas of the one shown.
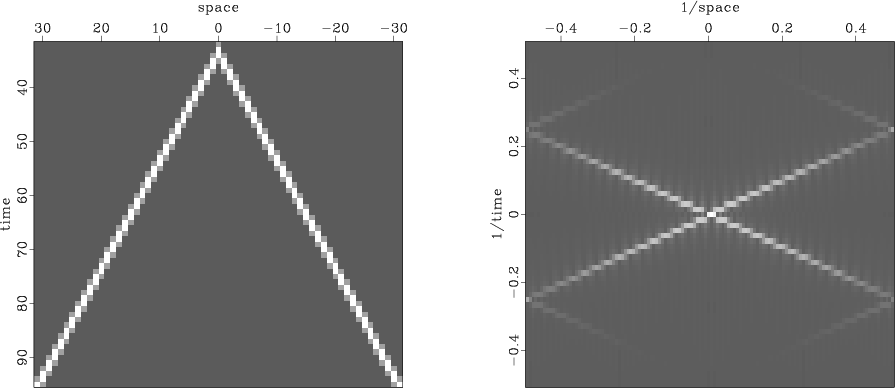
|
|---|
airwave
Figure 6.
A simulated air wave (left) and the amplitude of its FT (right).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
EXERCISES:
- Most time functions are real.
Their imaginary part is zero.
Show that this means that
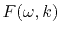 can
be determined from
can
be determined from
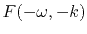 .
.
- What would change in Figure 5
if the pulse were moved
(a) earlier on the
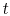 -axis, and
(b) further on the
-axis, and
(b) further on the 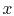 -axis?
What would change in Figure 5
if instead
the time axis were smoothed with (1,4,6,4,1)
and the space axis with (1,1)?
-axis?
What would change in Figure 5
if instead
the time axis were smoothed with (1,4,6,4,1)
and the space axis with (1,1)?
- What would Figure 6
look like on an earth with half the earth velocity?
- Numerically (or theoretically)
compute the two-dimensional spectrum
of a plane wave [
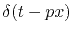 ], where
the plane wave has a randomly fluctuating amplitude:
say, rand
], where
the plane wave has a randomly fluctuating amplitude:
say, rand is a random number between
is a random number between 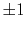 ,
and the randomly modulated plane wave is
[
,
and the randomly modulated plane wave is
[
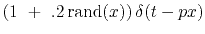 ].
].
- Explain the horizontal ``layering'' in Figure 4
in the plot of
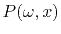 .
What determines the ``layer'' separation?
What determines the ``layer'' slope?
.
What determines the ``layer'' separation?
What determines the ``layer'' slope?
Next: Magic with 2-D Fourier
Up: SETTING UP 2-D FT
Previous: Signs in Fourier transforms
2013-01-06

![]() -axis.
We see a wave propagating in each direction
from the location of the source of the wave.
In Fourier space there are also two lines, one for each wave.
Notice that there are other lines which do not go through the origin;
these lines are called ``spatial aliases.''
Each actually goes through the origin
of another square plane that is not shown,
but which we can imagine alongside the one shown.
These other planes are periodic replicas of the one shown.
-axis.
We see a wave propagating in each direction
from the location of the source of the wave.
In Fourier space there are also two lines, one for each wave.
Notice that there are other lines which do not go through the origin;
these lines are called ``spatial aliases.''
Each actually goes through the origin
of another square plane that is not shown,
but which we can imagine alongside the one shown.
These other planes are periodic replicas of the one shown.