|
|
|
|
Waves and Fourier sums |
Signals go on and on, practically forever.
Sometimes we like to limit our attention to something more limited such
as their spectrum, or equivalently, their autocorrelation.
We can compute the autocorrelation in the Fourier domain.
We multiply the FT times its complex conjugate
![]() .
Transforming back to the physical domain we see Figure 8.
We expect a giant burst at zero offset (upper right corner).
We do not see it because it is "clipped",
i.e. plot values above some threshhold are plotted at that threshhold.
I could scale the plot to see the zero-offset burst,
but then the interesting signals shown here would be too weak to be seen.
.
Transforming back to the physical domain we see Figure 8.
We expect a giant burst at zero offset (upper right corner).
We do not see it because it is "clipped",
i.e. plot values above some threshhold are plotted at that threshhold.
I could scale the plot to see the zero-offset burst,
but then the interesting signals shown here would be too weak to be seen.
|
|---|
|
brad2
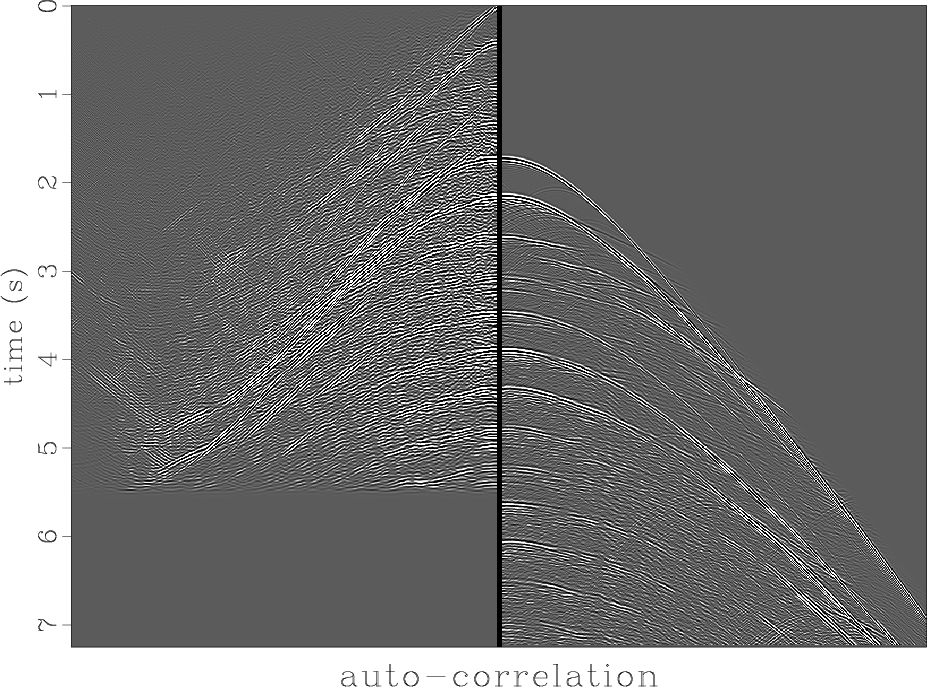
Figure 8. The 2-D autocorrelation of a shot profile resembles itself. |
|
|
Figure 8 shows us that the 2-D autocorrelation of a shot profile shares a lot in common with the shot profile itself. This is interesting news. If we had a better understanding of this we might find some productive applications. We might find a situation where we do not have (or do not want) the data itself but we do wish to build an earth model. For example, suppose we have permanently emplaced geophones. The earth is constantly excited by seismic noise. Some of it is man made; some results from earthquakes elsewhere in the world; most probably results from natural sources such as ocean waves, wind in trees, etc. Recall every bit of acoustic energy that arrives at the surface from below becomes a little bit of a source for a second reflection seismic experiment. So, by autocorrelating the data of hours and days duration we convert the chaos of continuing microseismic noise to something that might be the impulse response of the earth, or something like it. Autocorrelation converts a time axis of length of days to one of seconds. From the autocorrelation we might be able to draw conclusions in usual ways, alternately, we might learn how to make earth models from autocorrelations.
Notice from Figure 8 that since the first two seconds of the signal vanishes (travel time to ocean bottom), the last two seconds of the autocorrelation must vanish (longest nonzero lag on the data).
There are many issues on Figure 8 to intrigue an interpreter (starting with signal polarity). We also notice that the multiples on the autocorrelation die off rapidly with increasing offset and wonder why, and whether the same is true of primaries. But today is not the day to start down these paths.
In principal an autocorrelation is not comparable to the raw data or to the ideal shot profile because forming a spectrum squares amplitudes. We can overcome this difficulty by use of multidimensional spectral factorization -- but that's an advanced mathematical concept not defined in this book. See my other book, Image Estimation.
|
|
|
|
Waves and Fourier sums |