 |
 |
 |
 | Imaging in shot-geophone space |  |
![[pdf]](icons/pdf.png) |
Next: Zero-dip stacking (Y =
Up: Imaging in shot-geophone space
Previous: The DSR equation in
The double-square-root equation
is not easy to understand because it is an operator in a
four-dimensional space, namely, 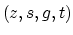 .
We will approach it through various applications, each of which is like a
picture in a space of lower dimension.
In this section lateral velocity variation will be neglected
(things are bad enough already!).
.
We will approach it through various applications, each of which is like a
picture in a space of lower dimension.
In this section lateral velocity variation will be neglected
(things are bad enough already!).
One way to reduce the dimensionality of (9.14)
is simply to set 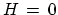 .
Then the two square roots become the same, so that they can be
combined to give the familiar paraxial equation:
.
Then the two square roots become the same, so that they can be
combined to give the familiar paraxial equation:
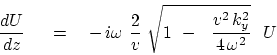 |
(32) |
In both places in equation (9.32) where the rock velocity occurs,
the rock velocity is divided by 2.
Recall that the rock velocity needed to be halved in order for field
data to correspond to the exploding-reflector model.
So whatever we did by setting 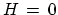 ,
gave us the same migration equation we used in chapter
,
gave us the same migration equation we used in chapter ![[*]](icons/crossref.png) .
Setting
.
Setting 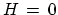 had the effect of making the survey-sinking concept
functionally equivalent to the exploding-reflector concept.
had the effect of making the survey-sinking concept
functionally equivalent to the exploding-reflector concept.
Subsections
 |
 |
 |
 | Imaging in shot-geophone space |  |
![[pdf]](icons/pdf.png) |
Next: Zero-dip stacking (Y =
Up: Imaging in shot-geophone space
Previous: The DSR equation in
2009-03-16
![]() .
We will approach it through various applications, each of which is like a
picture in a space of lower dimension.
In this section lateral velocity variation will be neglected
(things are bad enough already!).
.
We will approach it through various applications, each of which is like a
picture in a space of lower dimension.
In this section lateral velocity variation will be neglected
(things are bad enough already!).
![]() .
Then the two square roots become the same, so that they can be
combined to give the familiar paraxial equation:
.
Then the two square roots become the same, so that they can be
combined to give the familiar paraxial equation: