Next: Solution to kinematic equations
Up: DIPPING WAVES
Previous: Snell waves
Suppose the velocity increases to infinity at infinite depth.
Then equation (3.11) tells us that something
strange happens when we reach the depth for which
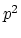 equals
equals 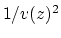 .
That is the depth at which the ray turns horizontal.
We will see in a later chapter that below this critical depth
the seismic wavefield damps exponentially with increasing depth.
Such waves are called evanescent.
For a physical example of an evanescent wave,
forget the airplane and think about a moving bicycle.
For a bicyclist, the slowness
.
That is the depth at which the ray turns horizontal.
We will see in a later chapter that below this critical depth
the seismic wavefield damps exponentially with increasing depth.
Such waves are called evanescent.
For a physical example of an evanescent wave,
forget the airplane and think about a moving bicycle.
For a bicyclist, the slowness 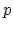 is so large that it dominates
is so large that it dominates 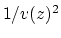 for all earth materials.
The bicyclist does not radiate a wave,
but produces a ground deformation
that decreases exponentially into the earth.
To radiate a wave,
a source must move faster than the material velocity.
for all earth materials.
The bicyclist does not radiate a wave,
but produces a ground deformation
that decreases exponentially into the earth.
To radiate a wave,
a source must move faster than the material velocity.
2009-03-16