 |
 |
 |
 | Time-shift imaging condition in seismic migration |  |
![[pdf]](icons/pdf.png) |
Next: Angle transformation in wave-equation
Up: Imaging condition in wave-equation
Previous: Time-shift imaging condition
To be even more general, we can formulate an imaging condition
involving both space-shift and time-shift,
followed by image extraction at zero time:
However, the cost involved in this transformation is large,
so this general form does not have immediate practical value.
Imaging conditions described by equations
(3)-(4) and
(6)-(7) are special cases of
equations (9)-(10)
for 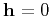 and
and 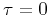 , respectively.
, respectively.
2013-08-29