 |
 |
 |
 | Elastic wave-mode separation for TTI media |  |
![[pdf]](icons/pdf.png) |
Next: Wave-mode separation for symmetry
Up: Wave-mode separation for 2D
Previous: Wave-mode separation for 2D
Dellinger and Etgen (1990) separate quasi-P
and quasi-SV modes in 2D VTI media by projecting the wavefields
onto the directions in which P and S modes are polarized. For
example, in the wavenumber domain, one can project the wavefields onto
the P-wave polarization vectors 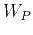 to obtain quasi-P (qP) waves:
to obtain quasi-P (qP) waves:
 |
(1) |
where
 is the P-wave mode in the wavenumber
domain,
is the P-wave mode in the wavenumber
domain,
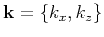 is the wavenumber vector,
is the wavenumber vector,
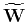 is the
elastic wavefield in the wavenumber domain, and
is the
elastic wavefield in the wavenumber domain, and
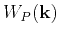 is the
P-wave polarization vector as a function of the wavenumber
is the
P-wave polarization vector as a function of the wavenumber 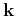 .
.
The polarization vectors
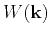 of plane waves for VTI media in
the symmetry planes can be found by solving the Christoffel equation
(Aki and Richards, 2002; Tsvankin, 2005):
of plane waves for VTI media in
the symmetry planes can be found by solving the Christoffel equation
(Aki and Richards, 2002; Tsvankin, 2005):
![$\displaystyle \left [{\bf G} - \rho V^2 {\bf I} \right]W= 0 ,$](img29.png) |
(2) |
where G is the Christoffel matrix with
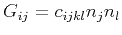 , in which
, in which 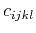 is the stiffness tensor.
The vector
is the stiffness tensor.
The vector
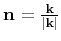 is the unit
vector orthogonal to the plane wavefront, with
is the unit
vector orthogonal to the plane wavefront, with 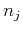 and
and  being
the components in the
being
the components in the 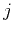 and
and 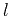 directions,
directions,
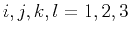 . The eigenvalues
. The eigenvalues 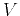 of this system correspond to the
phase velocities of different wave-modes and are dependent on the
plane wave propagation direction
of this system correspond to the
phase velocities of different wave-modes and are dependent on the
plane wave propagation direction  .
.
For plane waves in the vertical symmetry plane of a TTI medium, since
qP and qSV modes are decoupled from the SH-mode and
polarized in the symmetry planes, one can set  and obtain
and obtain
![$\displaystyle \left [ \mtrx{ G_{11}-\rho V^2 & G_{12}\ G_{12} & G_{22} -\rho V^2 } \right] \left [\mtrx{ U_x\ U_z} \right] =0 ,$](img41.png) |
(3) |
where
Equation 3 allows one to compute the polarization vectors
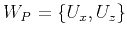 and
and
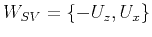 (the eigenvectors of the matrix
G) given the stiffness tensor at every location of the
medium.
(the eigenvectors of the matrix
G) given the stiffness tensor at every location of the
medium.
Equation 1 represents the separation process for the
P-mode in 2D homogeneous VTI media. To separate wave-modes for
heterogeneous models, one needs to use different polarization vectors at every
location of the model (Yan and Sava, 2009), because the polarization
vectors change spatially with medium parameters. In the space domain,
an expression equivalent to equation 1 at each grid point is
![$\displaystyle {\it q}P=\nabla_a\cdot \mathbf W= L_x[W_x] + L_z[W_z] ,$](img51.png) |
(7) |
where
![$ L\left [ \cdot \right]$](img52.png) indicates spatial filtering, and
indicates spatial filtering, and 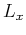 and
and 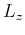 are the filters to separate P waves representing the inverse Fourier
transforms of
are the filters to separate P waves representing the inverse Fourier
transforms of 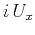 and
and  , respectively. The terms
, respectively. The terms 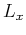 and
and 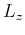 define the ``pseudo-derivative operators'' in the
define the ``pseudo-derivative operators'' in the  and
and 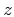 directions for a VTI medium, respectively, and they change according to the material
parameters,
directions for a VTI medium, respectively, and they change according to the material
parameters, 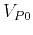 ,
, 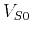 (
(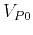 and
and 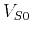 are the P and S
velocities along the symmetry axis, respectively),
are the P and S
velocities along the symmetry axis, respectively), 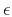 , and
, and
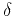 (Thomsen, 1986).
(Thomsen, 1986).
 |
 |
 |
 | Elastic wave-mode separation for TTI media |  |
![[pdf]](icons/pdf.png) |
Next: Wave-mode separation for symmetry
Up: Wave-mode separation for 2D
Previous: Wave-mode separation for 2D
2013-08-29
![]() of plane waves for VTI media in
the symmetry planes can be found by solving the Christoffel equation
(Aki and Richards, 2002; Tsvankin, 2005):
of plane waves for VTI media in
the symmetry planes can be found by solving the Christoffel equation
(Aki and Richards, 2002; Tsvankin, 2005):
![]() and obtain
and obtain