|
|
|
|
Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation |



|
|---|
|
slice,dipr,elpfr,delpfr
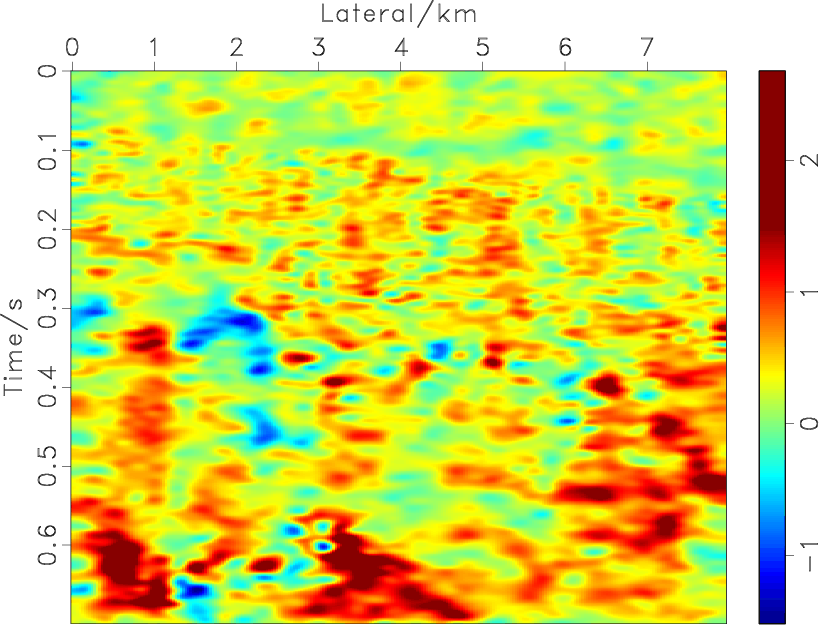
Figure 4. Comparison of processing results. Field data (a), Local dip (b), After filtering (c), Difference profile (d). |
|
|
For field data processing, we chose the 2D profile of 3D poststack data (Liu and Chen, 2013). The shallow structures are simple planar layers and the deep structures are complex curved layers. First, we use the proposed method, which is based on the 2D Hilbert transform, to compute the corresponding local seismic dip attribute (Figure 4b). From Figure 4b, we see that the dip changes smoothly and steadily in the midshallow layer corresponding to the continuous event in the profile, whereas the variation of the dip in the deep layer is relatively larger, which characterizes the bending event in the mid-deep layer.
The trend of the local seismic events can be determined by using the dip attribute; thus, we select the filtering window, which is determined by the dip, and use nonstationary polynomial fitting for filter processing. The window size of the structure-oriented data consists of 11 sampling points and the window size of the nonstationary polynomial fitting comprises seven sampling points.
Figure 4c shows the denoising results. We see that the random noise in the raw profile is suppressed, the whole section is clearer, and the continuity of the plane event (0.1s-0.3s) in the shallow layer and the curved event (below 0.3s) in the deep layer has improved. The difference profile (Figure 4d) shows that the removed noise is mainly irrelevant random noise and the information is well preserved.
|
|
|
|
Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation |