 |
 |
 |
 | Multi-dimensional Fourier transforms in the helical coordinate
system |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Theory
Previous: Wavenumber in helical coordinates
For a two-dimensional dataset with dimensions,
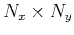 , the
cost of a 1-D FFT in helical coordinates is proportional to
, the
cost of a 1-D FFT in helical coordinates is proportional to
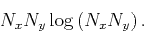 |
(20) |
For the same dataset, the cost of a 2-D FFT is
Therefore, the cost of a 1-D helical FFT of a 2-D dataset
is exactly the same as the cost of an 2-D FFT of the same dataset.
The link between the two leads to no computational advantages in the
number of operations.
However, other differences may lead to computational savings. For
example, a 2-D FFT with a power-of-two algorithm requires both 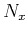 and
and 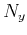 to be powers of two. However, the 1-D helical FFT requires
just
to be powers of two. However, the 1-D helical FFT requires
just 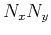 to be a power of two, and so less zero-padding may be
required.
to be a power of two, and so less zero-padding may be
required.
The corollary, that a large 1-D FFT
can be computed (with small inaccuracies) using a 2-D FFT algorithm,
also leads to potential computational savings.
Two-dimensional FFT's are easier to code to run both in parallel and
out-of-core than 1-D FFT's, leading to significantly faster code and a
lower memory requirement without the additional complexity of
Singleton's algorithm (Press et al., 1992).
 |
 |
 |
 | Multi-dimensional Fourier transforms in the helical coordinate
system |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Theory
Previous: Wavenumber in helical coordinates
2013-03-03
![]() and
and ![]() to be powers of two. However, the 1-D helical FFT requires
just
to be powers of two. However, the 1-D helical FFT requires
just ![]() to be a power of two, and so less zero-padding may be
required.
to be a power of two, and so less zero-padding may be
required.