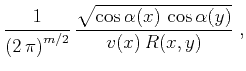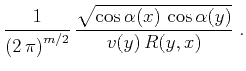|
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: Migration
Up: EXAMPLES
Previous: EXAMPLES
Let 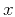 denote a point on the surface at which the propagating
wavefield is recorded. Let
denote a point on the surface at which the propagating
wavefield is recorded. Let 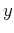 denote a point on another surface, to
which the wavefield is propagating. Then the summation path of the
stacking operator for the forward wavefield continuation is
denote a point on another surface, to
which the wavefield is propagating. Then the summation path of the
stacking operator for the forward wavefield continuation is
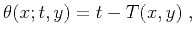 |
(32) |
where 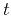 is the time recorded at the
is the time recorded at the 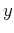 -surface, and
-surface, and 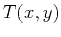 is the
traveltime along the ray connecting
is the
traveltime along the ray connecting 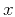 and
and 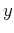 . The backward
propagation reverses the sign in (32), as follows:
. The backward
propagation reverses the sign in (32), as follows:
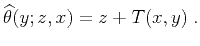 |
(33) |
Substituting the summation path formulas (32) and (33) into
the general weighting function formulas (28) and (29), we
immediately obtain
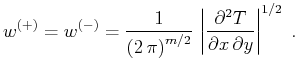 |
(34) |
Gritsenko's formula (Goldin, 1986; Gritsenko, 1984) states that the second mixed
traveltime derivative
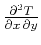 is connected with the geometric spreading
is connected with the geometric spreading 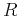 along the
along the 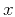 -
-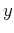 ray by
the equality
ray by
the equality
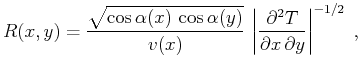 |
(35) |
where 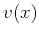 is the velocity at the point
is the velocity at the point 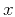 , and
, and 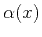 and
and
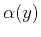 are the angles formed by the ray with the
are the angles formed by the ray with the 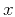 and
and 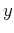 surfaces, respectively. In a constant-velocity medium,
surfaces, respectively. In a constant-velocity medium,
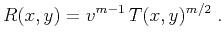 |
(36) |
Gritsenko's formula (35) allows us to
rewrite equation (34) in the form (Goldin, 1988)
The weighting functions commonly used in Kirchhoff datuming
(Wiggins, 1984; Berryhill, 1979; Goldin, 1985) are defined as
These two operators appear to be asymptotically inverse according to
formula (10). They coincide with the asymptotic pseudo-unitary
operators if the velocity 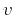 is constant (
is constant (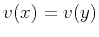 ), and the two
datum surfaces are parallel (
), and the two
datum surfaces are parallel (
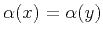 ).
).
 |
 |
 |
 | Asymptotic pseudounitary stacking operators |  |
![[pdf]](icons/pdf.png) |
Next: Migration
Up: EXAMPLES
Previous: EXAMPLES
2013-03-03