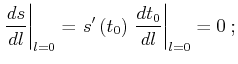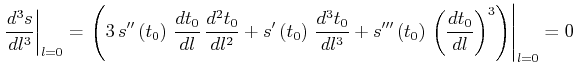|
 |
 |
 | Evaluating the Stolt-stretch parameter |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Evaluating the Stolt-stretch parameter
Previous: Acknowledgments
-
Alkhalifah, T., and I. Tsvankin, 1995, Velocity analysis for transversely
isotropic media: Geophysics, 60, 1550-1566.
-
-
Beasley, C., W. Lynn, K. Larner, and H. Nguyen, 1988, Cascaded
frequency-wavenumber migration - Removing the restrictions on depth-varying
velocity: Geophysics, 53, 881-893.
-
-
Castle, R. J., 1988, Shifted hyperbolas and normal moveout, in 58th
Annual Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts: Soc. Expl.
Geophys., Session: S9.3.
-
-
Claerbout, J. F., 1985, Imaging the Earth's Interior: Blackwell Scientific
Publications.
-
-
de Bazelaire, E., 1988, Normal moveout revisited - inhomogeneous media and
curved interfaces: Geophysics, 53, 143-157.
-
-
Fomel, S., 1997, Velocity continuation and the anatomy of prestack residual
migration: 67th Ann. Internat. Mtg, Soc. of Expl. Geophys., 1762-1765.
-
-
Fomel, S., and V. Grechka, 1996, On nonhyperbolic reflection moveout in
anisotropic media, in SEP-92: Stanford Exploration Project, 135-158.
-
-
Fomel, S. B., 1994, The method of velocity continuation in the seismic time
migration problem: Russian Geology and Geophysics, 35, 100-111.
-
-
Gazdag, J., 1978, Wave equation migration with the phase-shift method:
Geophysics, 43, 1342-1351.
-
-
Larner, K., and C. Beasley, 1987, Cascaded migrations - Improving the
accuracy of finite-difference migration: Geophysics, 52, 618-643.
- (Errata in GEO-52-8-1165).
-
Larner, K. L., C. J. Beasley, and W. S. Lynn, 1989, In quest of the flank:
Geophysics, 54, 701-717.
- (Erratum in GEO-54-7-932-932; Discussion in GEO-54-12-1648-1650 with
reply by authors).
-
Levin, S., 1983, Remarks on two-pass 3-D migration error, in SEP-35:
Stanford Exploration Project, 195-200.
-
-
----, 1985, Understanding Stolt stretch, in SEP-42: Stanford
Exploration Project, 373-374.
-
-
Malovichko, A. A., 1978, A new representation of the traveltime curve of
reflected waves in horizontally layered media: Applied Geophysics (in
Russian), 91, 47-53.
-
-
Popovici, A. M., F. Muir, and P. Blondel, 1996, Stolt redux: A new
interpolation method: Journal of Seismic Exploration, 5, 341-347.
-
-
Sava, P., 2000, Prestack Stolt residual migration for migration velocity
analysis, in 70th Annual Internat. Mtg., Soc. Expl. Geophys., Expanded
Abstracts: Soc. Expl. Geophys., 992-995.
-
-
Stolt, R. H., 1978, Migration by Fourier transform: Geophysics, 43,
23-48.
- (Discussion and reply in GEO-60-5-1583).
-
----, 1996, Short note - A prestack residual time migration operator:
Geophysics, 61, 605-607.
-
-
Sword, C. H., 1987, A Soviet look at datum shift, in SEP-51: Stanford
Exploration Project, 313-316.
-
-
Thomsen, L., 1986, Weak elastic anisotropy: Geophysics, 51, 1954-1966.
- (Discussion in GEO-53-04-0558-0560 with reply by author).
-
Yilmaz, Ö., 2001, Seismic data analysis: Processing, inversion, and
interpretation of seismic data: Soc. Expl. Geophys.
-
-
Yilmaz, Ö., I. Tanir, C. Gregory, and F. Zhou, 2001, Interpretive
imaging of seismic data: The Leading Edge, 20.
-
Appendix
A
In this Appendix, we derive an explicit expression for the
Stolt-stretch parameter 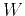 by comparing the accuracy of equations
(11) and (13), which approximate the
traveltime curve in the neighborhood of the vertical ray. It is
appropriate to consider a series expansion of the diffraction
traveltime in the vicinity of the vertical ray:
by comparing the accuracy of equations
(11) and (13), which approximate the
traveltime curve in the neighborhood of the vertical ray. It is
appropriate to consider a series expansion of the diffraction
traveltime in the vicinity of the vertical ray:
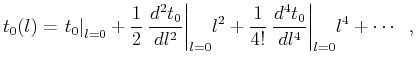 |
(24) |
where 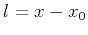 .
Expansion (A-1) contains only even powers of
.
Expansion (A-1) contains only even powers of 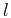 because of
the obvious symmetry of
because of
the obvious symmetry of 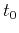 as a function of
as a function of 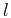 .
.
Matching the series expansions term by term is a constructive method
for relating different equations to each other. The special choice of
parameters 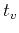 ,
, 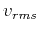 , and
, and 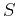 allows Malovichko's equation
(13) to provide correct values for the first three terms
of expansion (A-1):
allows Malovichko's equation
(13) to provide correct values for the first three terms
of expansion (A-1):
Considering Levin's equation (11) as an implicit
definition of the function
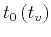 , we can iteratively
differentiate it, following the rules of calculus:
, we can iteratively
differentiate it, following the rules of calculus:
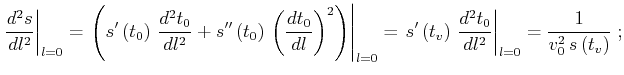 |
(28) |
Substituting the definition of Stolt stretch transform (5)
into (A-5) produces an equality similar to
(A-3), which means that approximation (11) is
theoretically accurate in depth-varying velocity media up to the
second term in (A-1). It is this remarkable property that
proves the validity of the Stolt stretch method
(Claerbout, 1985; Levin, 1983). Moreover, equation
(11) is accurate up to the third term if the value of the
fourth-order traveltime derivative in (A-6) coincides with
(A-4). Substituting equation (A-4) into
(A-6) results in the expression
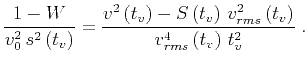 |
(30) |
It is now easy to derive from equation (A-7) the desired
explicit expression for the Stolt stretch parameter 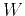 :
equation (17) in the main text.
:
equation (17) in the main text.
 |
 |
 |
 | Evaluating the Stolt-stretch parameter |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Evaluating the Stolt-stretch parameter
Previous: Acknowledgments
2014-03-29
![]() by comparing the accuracy of equations
(11) and (13), which approximate the
traveltime curve in the neighborhood of the vertical ray. It is
appropriate to consider a series expansion of the diffraction
traveltime in the vicinity of the vertical ray:
by comparing the accuracy of equations
(11) and (13), which approximate the
traveltime curve in the neighborhood of the vertical ray. It is
appropriate to consider a series expansion of the diffraction
traveltime in the vicinity of the vertical ray:
![]() ,
, ![]() , and
, and ![]() allows Malovichko's equation
(13) to provide correct values for the first three terms
of expansion (A-1):
allows Malovichko's equation
(13) to provide correct values for the first three terms
of expansion (A-1):