 |
 |
 |
 | New insights into one-norm solvers from the Pareto curve |  |
![[pdf]](icons/pdf.png) |
Next: Pareto curve
Up: Hennenfent et al.: Pareto
Previous: Introduction
Consider the following underdetermined system of linear
equations
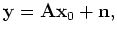 |
(1) |
where the 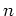 -vectors
-vectors
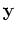 and
and
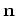 represent
observations and additive noise, respectively. The
represent
observations and additive noise, respectively. The 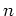 -by-
-by-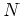 matrix
matrix
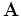 is the modeling operator that links the model
is the modeling operator that links the model
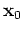 to the noise-free data given by
to the noise-free data given by
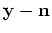 . We assume that
. We assume that 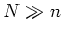 and that
and that
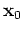 has few nonzero or significant entries. We use the
terms ``model'' and ``observations'' in a broad sense, so that many
linear geophysical problems can be cast in the form shown in
equation 1. In the case of wavefield reconstruction, for
example,
has few nonzero or significant entries. We use the
terms ``model'' and ``observations'' in a broad sense, so that many
linear geophysical problems can be cast in the form shown in
equation 1. In the case of wavefield reconstruction, for
example,
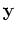 is the acquired seismic data with missing
traces,
is the acquired seismic data with missing
traces,
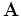 can be the restriction operator combined with the
curvelet synthesis operator so that
can be the restriction operator combined with the
curvelet synthesis operator so that
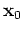 is the curvelet
representation of the fully-sampled wavefield
(Herrmann and Hennenfent, 2008; Hennenfent and Herrmann, 2008).
is the curvelet
representation of the fully-sampled wavefield
(Herrmann and Hennenfent, 2008; Hennenfent and Herrmann, 2008).
Because
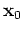 is assumed to be (almost) sparse, one can
promote sparsity as a prior via one-norm regularization to overcome
the singular nature of
is assumed to be (almost) sparse, one can
promote sparsity as a prior via one-norm regularization to overcome
the singular nature of
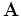 when estimating
when estimating
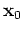 from
from
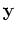 . A common approach is to solve the convex
optimization problem
. A common approach is to solve the convex
optimization problem
QP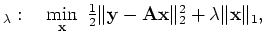 |
|
which is closely related to quadratic programming (QP); the positive
parameter 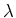 is the Lagrange multiplier, which balances the
tradeoff between the two norm of the data misfit and the one norm of
the solution. Many algorithms are available for solving QP
is the Lagrange multiplier, which balances the
tradeoff between the two norm of the data misfit and the one norm of
the solution. Many algorithms are available for solving QP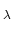 ,
including IRLS, iterative soft thresholding (IST), introduced by
Daubechies et al. (2004), and the IST extension to include cooling (ISTc
- Figueiredo and Nowak, 2003), which was tailored to geophysical applications by
Herrmann and Hennenfent (2008).
,
including IRLS, iterative soft thresholding (IST), introduced by
Daubechies et al. (2004), and the IST extension to include cooling (ISTc
- Figueiredo and Nowak, 2003), which was tailored to geophysical applications by
Herrmann and Hennenfent (2008).
It is generally not clear, however, how to choose the parameter
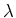 such that the solution of QP
such that the solution of QP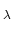 is, in some sense,
optimal. A directly related optimization problem, the basis pursuit
(BP) denoise problem (Chen et al., 1998), minimizes the one norm of
the solution given a maximum misfit, and is given by
is, in some sense,
optimal. A directly related optimization problem, the basis pursuit
(BP) denoise problem (Chen et al., 1998), minimizes the one norm of
the solution given a maximum misfit, and is given by
BP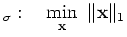 s.t. s.t.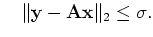 |
|
This formulation is often preferred when an estimate of the noise
level
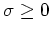 in the data is available. BP
in the data is available. BP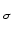 can be
solved using ISTc or the spectral projected-gradient algorithm
(SPG
can be
solved using ISTc or the spectral projected-gradient algorithm
(SPG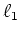 ) introduced by van den Berg and Friedlander (2008).
) introduced by van den Berg and Friedlander (2008).
For interest, a third optimization problem, connected to QP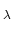 and BP
and BP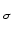 , minimizes the misfit given a maximum one norm of the
solution, and is given by the LASSO (LS) problem
(Tibshirani, 1996)
, minimizes the misfit given a maximum one norm of the
solution, and is given by the LASSO (LS) problem
(Tibshirani, 1996)
LS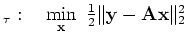 s.t. s.t.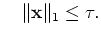 |
|
Because an estimate of the one norm of the solution
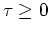 is
typically not available for geophysical problems, this formulation is
seldom used directly. It is, however, a key internal problem used by
SPG
is
typically not available for geophysical problems, this formulation is
seldom used directly. It is, however, a key internal problem used by
SPG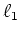 in order to solve BP
in order to solve BP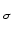 .
.
To understand the connection between these approaches and compare
their related solvers in different scenarios, we propose to follow
Daubechies et al. (2007) and van den Berg and Friedlander (2008) and look at the Pareto curve.
 |
 |
 |
 | New insights into one-norm solvers from the Pareto curve |  |
![[pdf]](icons/pdf.png) |
Next: Pareto curve
Up: Hennenfent et al.: Pareto
Previous: Introduction
2008-03-27
![]() is assumed to be (almost) sparse, one can
promote sparsity as a prior via one-norm regularization to overcome
the singular nature of
is assumed to be (almost) sparse, one can
promote sparsity as a prior via one-norm regularization to overcome
the singular nature of
![]() when estimating
when estimating
![]() from
from
![]() . A common approach is to solve the convex
optimization problem
. A common approach is to solve the convex
optimization problem
![]() such that the solution of QP
such that the solution of QP![]() is, in some sense,
optimal. A directly related optimization problem, the basis pursuit
(BP) denoise problem (Chen et al., 1998), minimizes the one norm of
the solution given a maximum misfit, and is given by
is, in some sense,
optimal. A directly related optimization problem, the basis pursuit
(BP) denoise problem (Chen et al., 1998), minimizes the one norm of
the solution given a maximum misfit, and is given by
![]() and BP
and BP![]() , minimizes the misfit given a maximum one norm of the
solution, and is given by the LASSO (LS) problem
(Tibshirani, 1996)
, minimizes the misfit given a maximum one norm of the
solution, and is given by the LASSO (LS) problem
(Tibshirani, 1996)