 |
 |
 |
 | Angle gathers in wave-equation imaging for transversely isotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Conclusions
Up: Angle gathers in wave-equation
Previous: Synthetic Example
In the case of a tilt in the angle of symmetry of the TI (TTI) medium, the dispersion relations 2 and 3
must be altered to reflect the tilt. Specifically, the wavenumbers should be transformed
to the direction of the tilt. In fact, at the reflection point all equations used to develop the mapping in equation (4)
hold regardless of the direction of tilt. This implies that the
quadratic solution (5) applies with 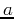 ,
, 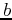 , and
, and 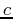 given by Table 1 granted that the wavenumbers are transformed in the direction of the tilt.
Considering that
given by Table 1 granted that the wavenumbers are transformed in the direction of the tilt.
Considering that 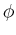 is the tilt angle measured from vertical in 2-D, the horizontal (conventional) wavenumbers given by the surface-recorded data
are given by
is the tilt angle measured from vertical in 2-D, the horizontal (conventional) wavenumbers given by the surface-recorded data
are given by
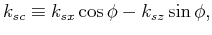 |
(6) |
and
 |
(7) |
where  and
and 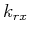 now correspond to the normal-to-the-tilt wavenumber direction and they are related to
now correspond to the normal-to-the-tilt wavenumber direction and they are related to 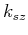 and
and 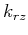 (tilt direction wavenumbers),
respectively using equations 2 and 3.
Based on the above equations, to solve for
(tilt direction wavenumbers),
respectively using equations 2 and 3.
Based on the above equations, to solve for  and
and 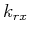 needed for the angle gather mapping, we are required to solve a quartic equation that can be represented, with pain, analytically
or solved numerically. Alternatively, the formulations for a transversely isotropic medium with tilt constrained to the dip (DTI), introduced by Alkhalifah and Sava (2010), is
simpler than those introduced here for a general TI medium, and thus can be used at the velocity model building stage. However, when the assumption of the tilt being normal to the reflector dip
fails, for example at salt
flank reflections where the tilt is generally not normal to the Salt flank, we will need a general formulation similar to the one developed here.
needed for the angle gather mapping, we are required to solve a quartic equation that can be represented, with pain, analytically
or solved numerically. Alternatively, the formulations for a transversely isotropic medium with tilt constrained to the dip (DTI), introduced by Alkhalifah and Sava (2010), is
simpler than those introduced here for a general TI medium, and thus can be used at the velocity model building stage. However, when the assumption of the tilt being normal to the reflector dip
fails, for example at salt
flank reflections where the tilt is generally not normal to the Salt flank, we will need a general formulation similar to the one developed here.
 |
 |
 |
 | Angle gathers in wave-equation imaging for transversely isotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Conclusions
Up: Angle gathers in wave-equation
Previous: Synthetic Example
2013-04-02
![]() ,
, ![]() , and
, and ![]() given by Table 1 granted that the wavenumbers are transformed in the direction of the tilt.
Considering that
given by Table 1 granted that the wavenumbers are transformed in the direction of the tilt.
Considering that ![]() is the tilt angle measured from vertical in 2-D, the horizontal (conventional) wavenumbers given by the surface-recorded data
are given by
is the tilt angle measured from vertical in 2-D, the horizontal (conventional) wavenumbers given by the surface-recorded data
are given by