|
|
|
|
An eikonal based formulation for traveltime perturbation with respect to the source location |
Since the differential equation depends on velocity changes in the
direction of the source shift, we test the methodology on a model that
contains a lens anomaly in an otherwise constant velocity gradient
(
![]() and
and
![]() with
velocity at the origin equal to 2 km/s) model. The lens is located at
600 meters laterally and 500 meters depth with a velocity perturbation
of +500 m/s (or 20%). The lens has a diameter of 200 meters and
causes a large velocity variation. Using this model, we test the
accuracy of the first-order, second-order, and the Shanks-transform
representation equations.
with
velocity at the origin equal to 2 km/s) model. The lens is located at
600 meters laterally and 500 meters depth with a velocity perturbation
of +500 m/s (or 20%). The lens has a diameter of 200 meters and
causes a large velocity variation. Using this model, we test the
accuracy of the first-order, second-order, and the Shanks-transform
representation equations.
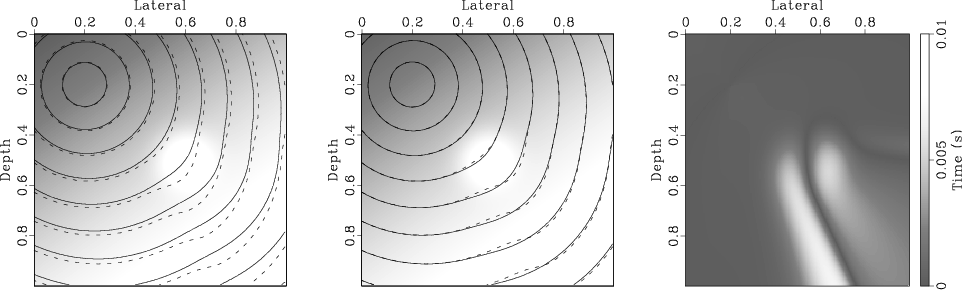
For a source located at 200 meters lateral distance from origin and
200 meter depth, we solve the eikonal equation using the fast marching
method with second order accuracy. The traveltime field in this case is
represented by the solid contours on the left side plots of
Figures 4, 5, and 6. We
also solve the eikonal equation for source located virtually 100
meters away in lateral direction and it is represented by the solid curves in the
middle plot of the three Figures. Solving for ![]() using
equation 3 and using that along with the original
traveltime field, we obtain an approximate traveltime field for a
source 100 meters away. This new traveltime field is represented by
the dashed contour curves in Figure 4. The absolute
difference between the simulated traveltime and the true one both
displayed in the center plot is given by the density plot shown on the
right side of Figure 4.
using
equation 3 and using that along with the original
traveltime field, we obtain an approximate traveltime field for a
source 100 meters away. This new traveltime field is represented by
the dashed contour curves in Figure 4. The absolute
difference between the simulated traveltime and the true one both
displayed in the center plot is given by the density plot shown on the
right side of Figure 4.
|
|---|
|
circ1
Figure 4. The traveltime contour (solid curve) plot for a source at lateral and depth position of 0.2 km (left) and for a source virtually perturbed by 100 meters in the lateral direction (middle), both compared with the traveltime derived using the first-order accuracy perturbation eikonal for a 100 meters virtual shift (dashed curves). In both plots the velocity field is shown in the background. Also shown on the right is a density plot of the difference between the two contours in the middle plot. |
|
|
The errors are generally small (less than 0.008 s), with the largest of errors appearing on the lower side of the lens. This error is generally small considering the large shift (100 meters) and first-order nature of the expansion. In addition, errors for the rest of the traveltime field corresponding to the linear variation in velocity is extremely small.
|
|---|
|
circ2
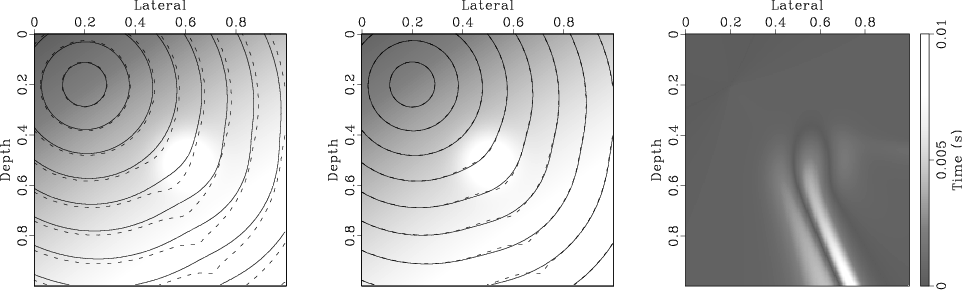
Figure 5. The traveltime contour (solid curve) plot for the original source (left) and for a source virtually perturbed by 100 meters in the lateral (middle), both compared with the traveltime derived using the second-order accuracy perturbation eikonal for a 100 meters virtual shift (dashed curves). In both plots the velocity field is shown in the background. Also shown on the right is a density plot of the difference between the two contours in the middle plot. |
|
|
Figure 5 is similar to Figure 4, but now we use the second-order expansion, which requires solving the linear partial differential equation twice. Overall, as expected, the errors are less than the first order case with clear reduction in the upper side trail of the lens.
|
|---|
|
circ3
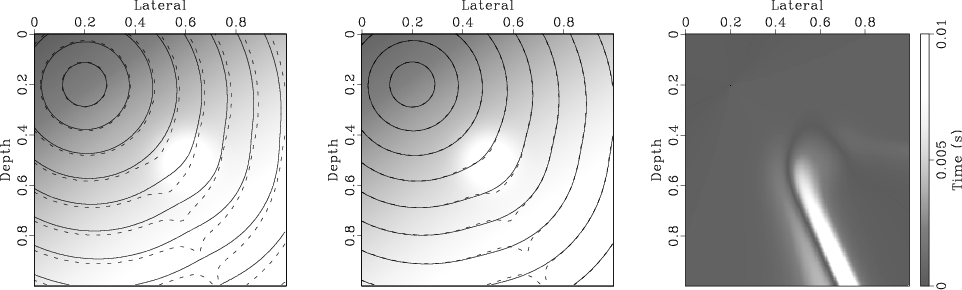
Figure 6. The traveltime contour (solid curve) plot for the original source (left) and for a source virtually perturbed by 100 meters (middle), both compared with the traveltime derived using Shanks transform perturbation eikonal for a 100 meters virtual shift (dashed curves). In both plots the velocity field is shown in the background. Also shown on the right is a density plot of the difference between the two contours in the middle plot. |
|
|
With hardly any additional computational cost, we can use the Shank transform representation of the expansion and in this case the errors, as shown in Figure 6, are reduced even further.
|
|---|
|
circ4
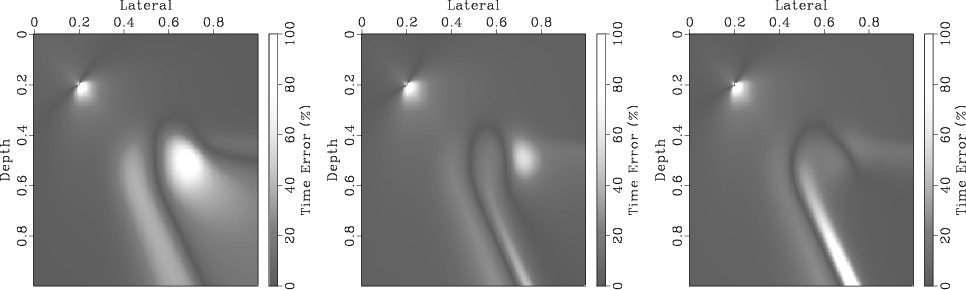
Figure 7. A density plot of the traveltime error in percent for the difference plots in Figures 4-6 (right), plotted from left to right, respectively. The percent error is measured in a relative manner where 0 corresponds to the accurate traveltime and 100% to the unperturbed traveltime. |
|
|
|
|
|
|
An eikonal based formulation for traveltime perturbation with respect to the source location |