|
|
|
|
An eikonal based formulation for traveltime perturbation with respect to the source location |
Despite the fact that the source perturbation differential equations are dependent on the derivative of velocity, and thus, discontinuous velocity fields pose a problem, we test the method on the unsmoothed Marmousi model (Versteeg, 1994) to asses the stability of the numerical process. In this case, we use only the first order expansion to avoid relying on higher order derivatives of the velocity field, which might breakdown here.
Figure 8 shows the Marmousi model in the background with the traveltime field contours computed directly using the finite difference eikonal equation for a source located at 4.2 km at the surface (dashed curves) compared with the traveltime field perturbed from a source located 200 meters away at 4 km surface location. The two contour curves overlap near the source, but show some difference away from the source. However, the difference is generally small considering the large source perturbation of 200 meters and the velocity complex model.

|
|---|
|
cir1
Figure 8. The traveltime contour plot for a source at the surface at 4.2 km (dashed curves) and for a source virtually perturbed by 200 meters from the traveltime field at 4 km source surface location (solid curves). The perturbed traveltime is derived using the first-order accuracy perturbation eikonal. The Marmousi velocity field is shown in the background. |
|
|
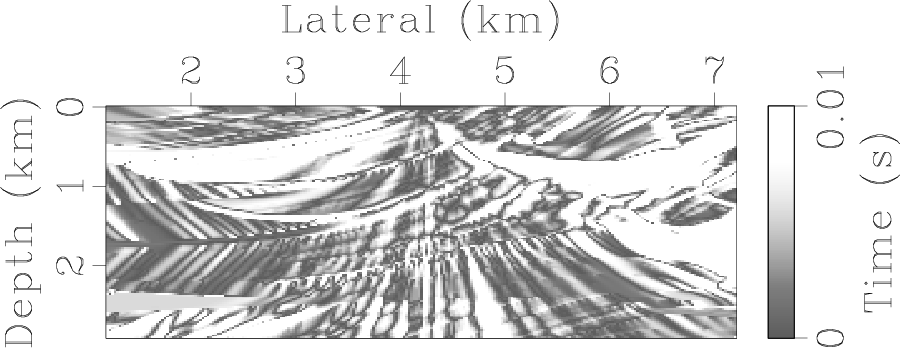
A closer and more quantitative look is given by the difference plot; Figure 9 shows a density plot for the difference in traveltime contours in Figure 8. With a clip of 0.01 seconds, errors given in gray are small and dominate the plot. This is a testament to the stability of the Fast marching implementation despite the complex velocity field that includes many lateral discontinuities.
|
|---|
|
cir2
Figure 9. A density plot for the difference between the two contours shown in Figure 8. |
|
|
|
|
|
|
An eikonal based formulation for traveltime perturbation with respect to the source location |