|
|
|
|
Seismic data interpolation beyond aliasing using regularized nonstationary autoregression |
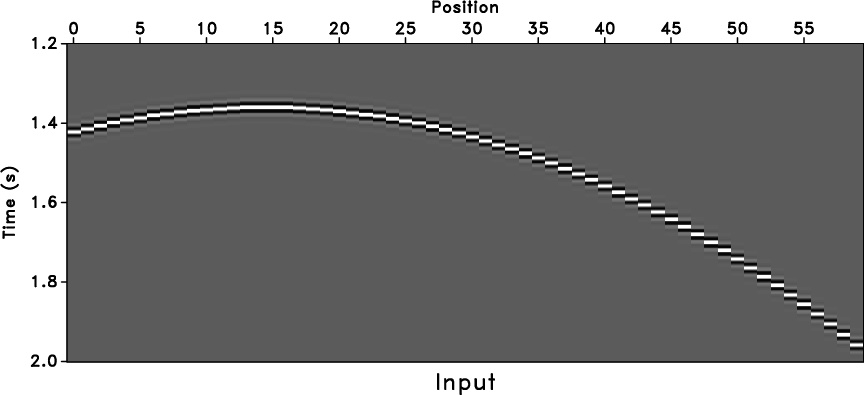
A benchmark example created by Raymond Abma (personal communication)
shows a simple curved event
(Figure 2a). The challenge in this
example is to account for both nonstationarity and
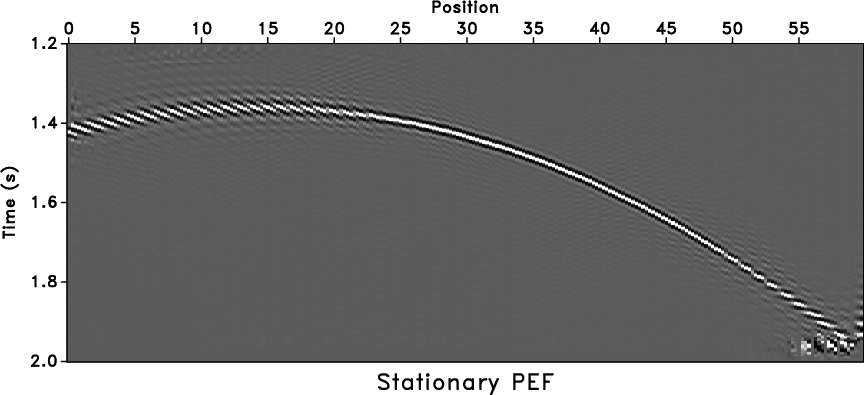
aliasing. Figure 2b shows the
interpolated result using Claerbout's stationary ![]() -
-![]() PEF, which
was estimated and applied in one big window, with each PEF coefficient
PEF, which
was estimated and applied in one big window, with each PEF coefficient
![]() constant at every data location. Note that the
constant at every data location. Note that the ![]() -
-![]() PEF
method can recover the aliasing trace only in the dominant slope
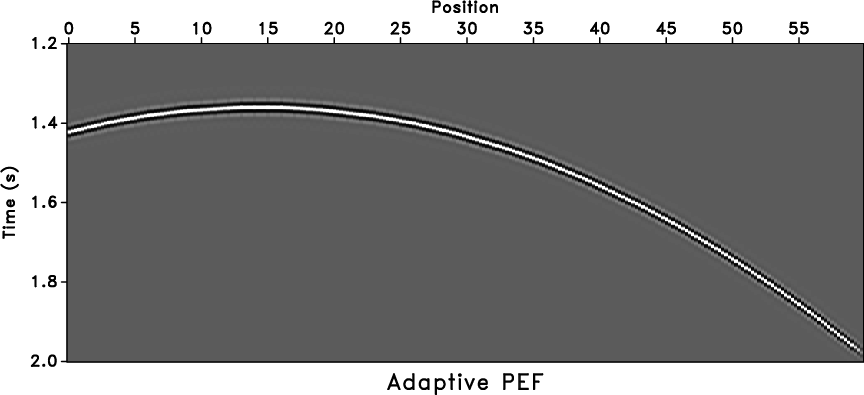
range. The trace-interpolating result using regularized nonstationary
autoregression is shown in Figure 2c. The
adaptive PEF has 20 (time)
PEF
method can recover the aliasing trace only in the dominant slope
range. The trace-interpolating result using regularized nonstationary
autoregression is shown in Figure 2c. The
adaptive PEF has 20 (time) ![]() 3 (space) coefficients for each
sample and a 20-sample (time)
3 (space) coefficients for each
sample and a 20-sample (time) ![]() 3-sample (space) smoothing
radius. The proposed method eliminates all nonstationary aliasing and
improves the continuity of the curved event.
3-sample (space) smoothing
radius. The proposed method eliminates all nonstationary aliasing and
improves the continuity of the curved event.
|
|---|
|
jcurve,jcscov,jcacov
Figure 2. Curve model (a), trace interpolation with stationary PEF (b), and trace interpolation with adaptive PEF (c). |
|
|
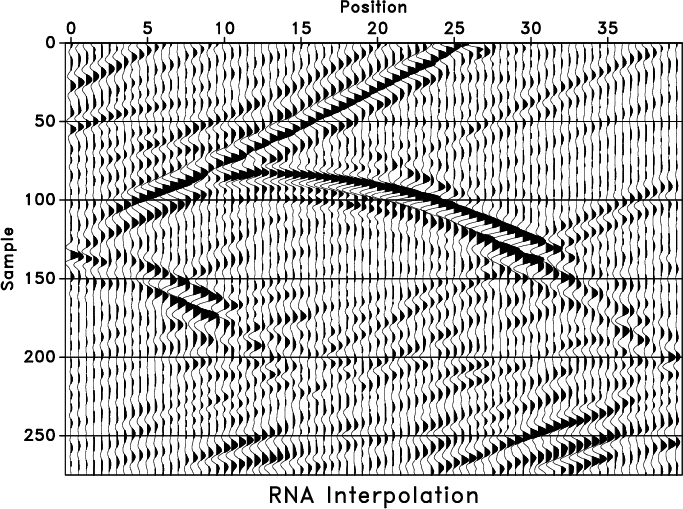
Abma and Kabir (2005) present a comparison of several algorithms used for
trace interpolation. We chose the most challenging benchmark Marmousi
example from Abma and Kabir to illustrate the performance of RNA
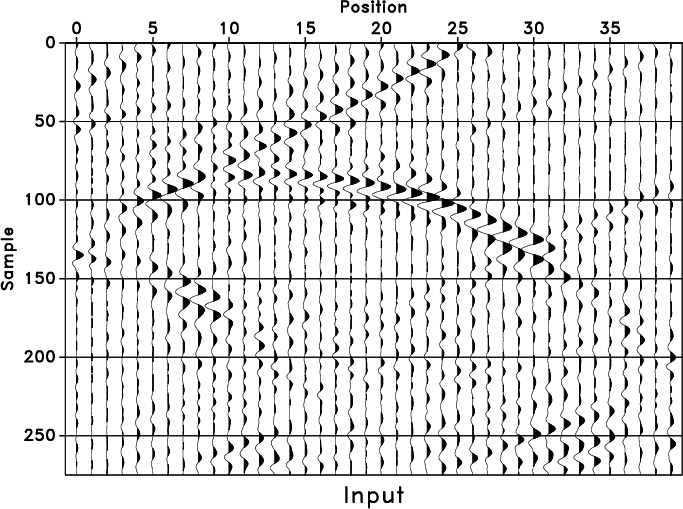
interpolation. Figure 3a shows a zero-offset
section of the Marmousi model, in which curved events violate the
assumptions common for most trace-interpolating
methods. Figure 3b shows that our method produces
reasonable results for both curved and weak events and does not
introduce any undesirable noise. The adaptive PEF parameters
correspond to 7 (time) ![]() 5 (space) coefficients for each sample
and a 40-sample (time)
5 (space) coefficients for each sample
and a 40-sample (time) ![]() 30-sample (space) smoothing radius.
30-sample (space) smoothing radius.
|
|---|
|
jmarm,jmacov
Figure 3. Marmousi model (a) and trace interpolation with regularized nonstationary autoregression (b). |
|
|
|
|
|
|
Seismic data interpolation beyond aliasing using regularized nonstationary autoregression |