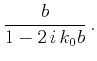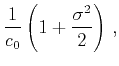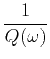|
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Browaeys & Fomel: Fractals
Previous: Conclusions
We thank Apache Canada Ltd. for providing the data used in this study and Mark Tomasso
from the Bureau of Economic Geology for the velocity model.
We acknowledge Apache Corporation, GX Technology Corporation,
and the Jackson School of Geosciences for financial support.
This publication is authorized by the Director, Bureau of Economic Geology,
The University of Texas at Austin.
Appendix
A
O'Doherty-Anstey formula and the mean field theory
O'Doherty and Anstey (O'Doherty and Anstey, 1971; Resnick, 1990) proposed
that local transmission coefficient 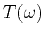 for traveltime
for traveltime 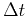 in sedimentary layers
should be
in sedimentary layers
should be
![$\displaystyle T(\omega) = \exp\left[-\frac{\omega\,\Delta t}{2\,Q(\omega)}\right] = e^{-R(\omega)\,\Delta t},$](img233.png) |
|
|
(41) |
where 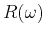 is the spectrum of reflection coefficients, which is related to the spectrum
of impedance fluctuations (Banik et al., 1985).
Because we have used velocity fluctuations, attenuation in the dispersion relation of equation 21
depends on the velocity spectrum:
is the spectrum of reflection coefficients, which is related to the spectrum
of impedance fluctuations (Banik et al., 1985).
Because we have used velocity fluctuations, attenuation in the dispersion relation of equation 21
depends on the velocity spectrum:
These formulae have been previously derived and analyzed (Lerche, 1986; Wu, 1988; Sato and Fehler, 1998).
The term 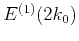 can be interpreted as backward scattering
with exchange wavenumber
can be interpreted as backward scattering
with exchange wavenumber 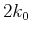 , whereas the term
, whereas the term 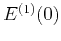 is forward scattering
with exchange wavenumber
is forward scattering
with exchange wavenumber 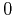 .
Both energy terms reduce to 1D expressions because of isotropic integration,
whereas one symmetry axis is imposed by propagation direction of the wave.
Further interpretation can be found using a dynamic effective model
for multiple scattering (Waterman and Truell, 1961):
the scattered waves interfere with the main wavefield,
and their relative phase continuously changes in all directions,
except for significant interferences in forward and backward directions.
Previous 1D derivations (Sato and Fehler, 1998)
have incorporated a traveltime correction, corresponding to neglecting forward scattering
in order to reproduce the O'Doherty-Anstey formula. This approach extends validity of the analytical expressions
to higher frequencies, but no simple traveltime phase correction exists for the mean field theory in 3D.
Constant
.
Both energy terms reduce to 1D expressions because of isotropic integration,
whereas one symmetry axis is imposed by propagation direction of the wave.
Further interpretation can be found using a dynamic effective model
for multiple scattering (Waterman and Truell, 1961):
the scattered waves interfere with the main wavefield,
and their relative phase continuously changes in all directions,
except for significant interferences in forward and backward directions.
Previous 1D derivations (Sato and Fehler, 1998)
have incorporated a traveltime correction, corresponding to neglecting forward scattering
in order to reproduce the O'Doherty-Anstey formula. This approach extends validity of the analytical expressions
to higher frequencies, but no simple traveltime phase correction exists for the mean field theory in 3D.
Constant 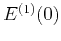 ensures recovery of the Backus effective medium and the Rayleigh diffusion regime for very low frequencies.
ensures recovery of the Backus effective medium and the Rayleigh diffusion regime for very low frequencies.
Appendix
B
Exponentially correlated heterogeneities
Results have been derived several times (Karal and Keller, 1964; Sato and Fehler, 1998)
using exponential correlation function
![$N(r)=\exp[-r/b]$](img243.png) and are added here as a specific case
with simple analytical expressions within the general framework of von Kármán's media.
Values of the integral in equation 22 are
and are added here as a specific case
with simple analytical expressions within the general framework of von Kármán's media.
Values of the integral in equation 22 are
Using these expressions in the dispersion relation of equation 21, the new dispersion relation, phase velocity 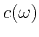 , and attenuation are
, and attenuation are
In the limit of very long wavelengths, i.e.
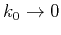 ,
attenuation and velocity reduce respectively to the Rayleigh diffusion
regime and the effective medium theory of Backus (1962):
,
attenuation and velocity reduce respectively to the Rayleigh diffusion
regime and the effective medium theory of Backus (1962):
 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Browaeys & Fomel: Fractals
Previous: Conclusions
2013-07-26
![]() for traveltime
for traveltime ![]() in sedimentary layers
should be
in sedimentary layers
should be
![$\displaystyle T(\omega) = \exp\left[-\frac{\omega\,\Delta t}{2\,Q(\omega)}\right] = e^{-R(\omega)\,\Delta t},$](img233.png)
![]() and are added here as a specific case
with simple analytical expressions within the general framework of von Kármán's media.
Values of the integral in equation 22 are
and are added here as a specific case
with simple analytical expressions within the general framework of von Kármán's media.
Values of the integral in equation 22 are