|
|
|
|
Non-hyperbolic common reflection surface |
In this appendix, we reproduce the derivation of an analytical expression for reflection traveltime from a hyperbolic reflector in a homogeneous velocity model (Fomel and Stovas, 2010). Similar derivations apply to an elliptic reflector and were used previously in the theory of offset continuation (Stovas and Fomel, 1996; Fomel, 2003).
Consider the source point ![]() and the receiver point
and the receiver point ![]() at the
surface
at the
surface ![]() above a 2-D constant-velocity medium and a hyperbolic
reflector defined by the equation
above a 2-D constant-velocity medium and a hyperbolic
reflector defined by the equation
has physical meaning. Substituting this solution into equation (A-2), we obtain, after a number of algebraic simplifications,
The connection with the multifocusing parameters is summarized in Table 1 for the general case and three special cases (a plane dipping reflector, a flat reflector, and a point diffractor). The first two special cases turn the nonhyperbolic CRS equation into the hyperbolic form (8). The last case turns it into the double-square-root form (13).
|
|
||||
| Hyperbolic reflector |
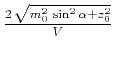
|
|
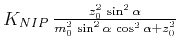
|
|
| Plane dipping reflector | ||||
|
|
|
0 |
|
|
| Flat reflector | ||||
|
|
|
0 | 0 | |
| Point diffractor | ||||
|
|

|
|
|
|
|
|
|
Non-hyperbolic common reflection surface |