|
|
|
|
Compressive sensing for seismic data reconstruction via fast projection onto convex sets based on seislet transform |
Next: Discussions Up: Gan et al.: Compressive Previous: Comparison of sparsity-promoting transforms
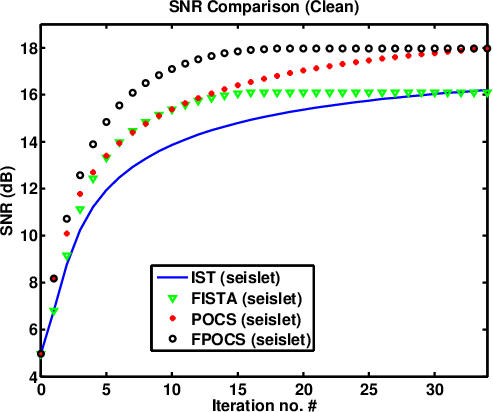
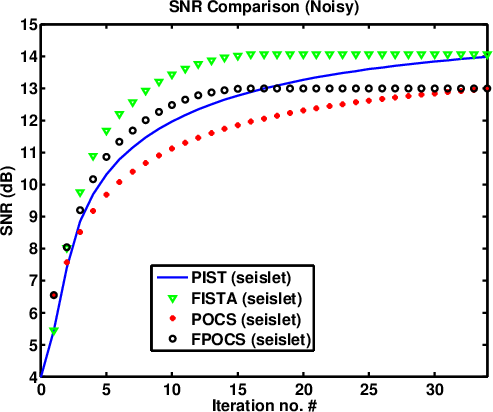
In order to compare the difference between IST and POCS (or between FPOCS and FISTA). We do two experiments with clean and noisy irregularly sampled datasets, respectively. For the clean data case, we use the same synthetic example as shown in Figures 3a and 12a. We reconstruct the missing data with seislet POCS, seislet FPOCS, seislet IST, seislet FISTA, and show the convergence diagrams in terms of SNR in Figure 12b. It is obvious that both seislet POCS and seislet FPOCS obtain better converged results than seislet IST and seislet FISTA, which results from the fact that in POCS based methods the sampled clean data components help constrain the model during the inversion. However, for the noisy data case, as shown in Figure 12c, the convergence diagrams show opposite performance compared with the clean data case. Both seislet POCS and seislet FPOCS obtain better converged results than seislet IST and seislet FISTA. This phenomenon results from the fact that during the inversion, the IST based methods can help remove the random noise iteratively while the POCS based approaches maintain the random noise in the known data components. The conclusion from these two experiments can guide us to decide which type of method (POCS or IST) to use in practice according to the level of noise existing in the seismic data: for relatively noisier dataset, the IST (FISTA) method can be superior because during the thresholding process, the extra random noise will be attenuated gradually; for relatively cleaner dataset, the POCS (FPOCS) method can be superior because the known sampled data help constrain the spatial coherency during the inversion. Currently, we do not have ways to quantify the noise level acceptable for FPOCS. It might be an interesting topic for future investigation.. The next field data example is from a marine survey, with high data quality, thus we keep using the POCS based approach for comparison
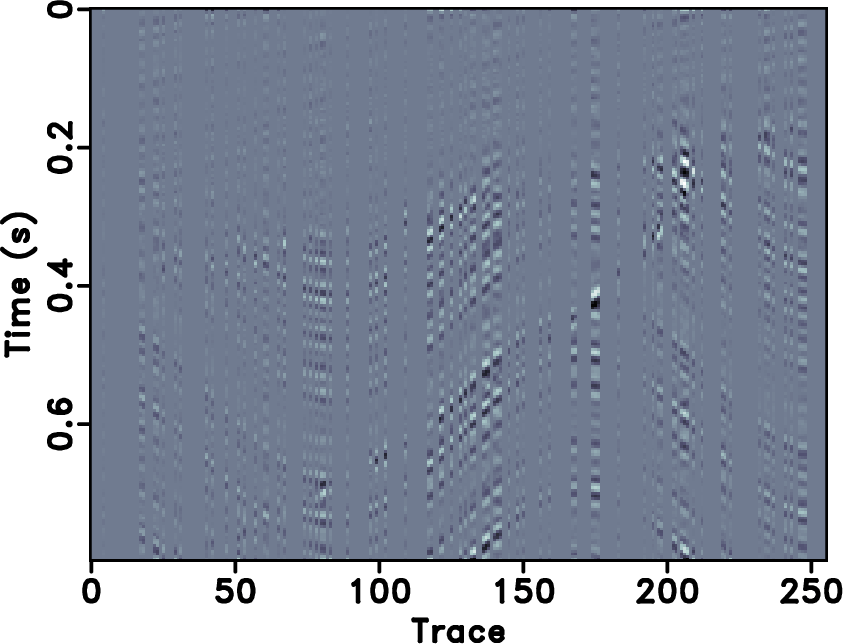
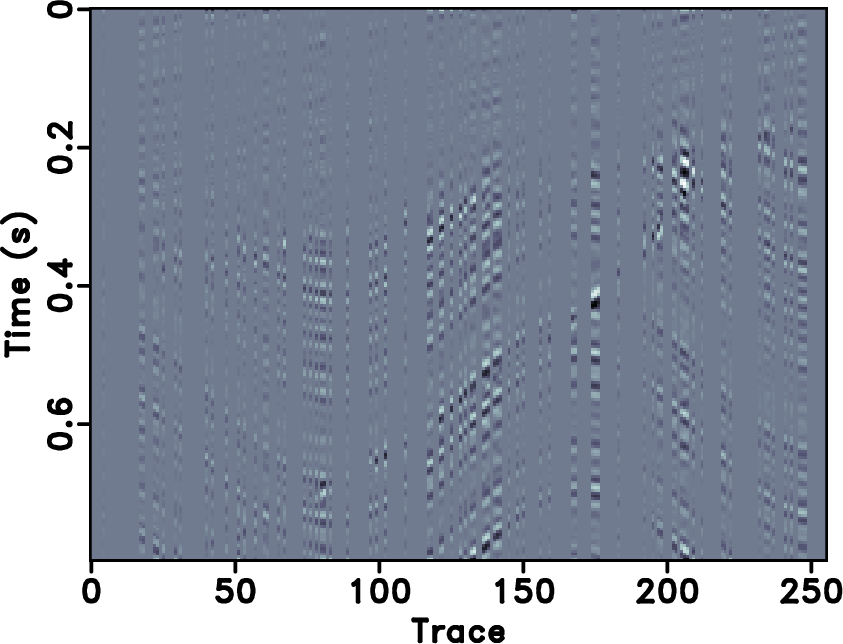
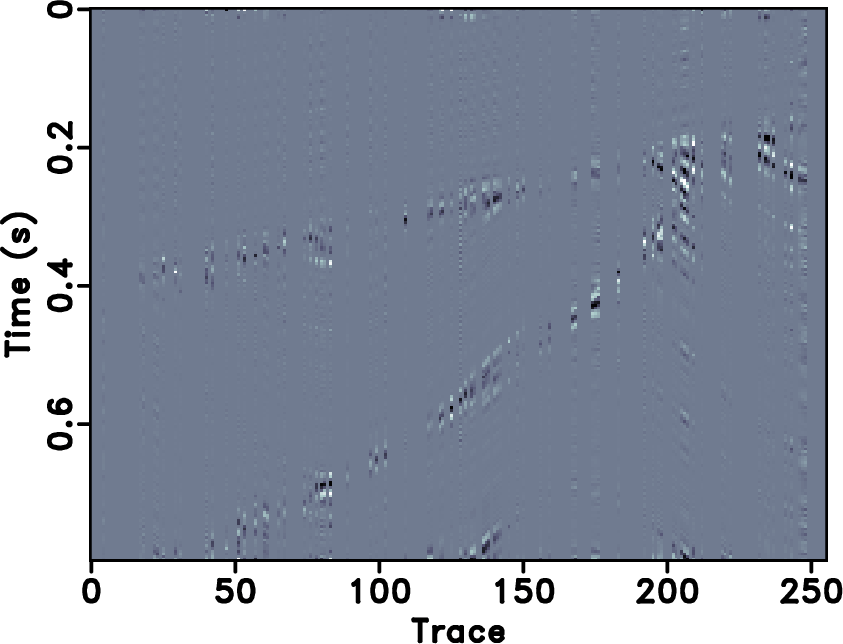
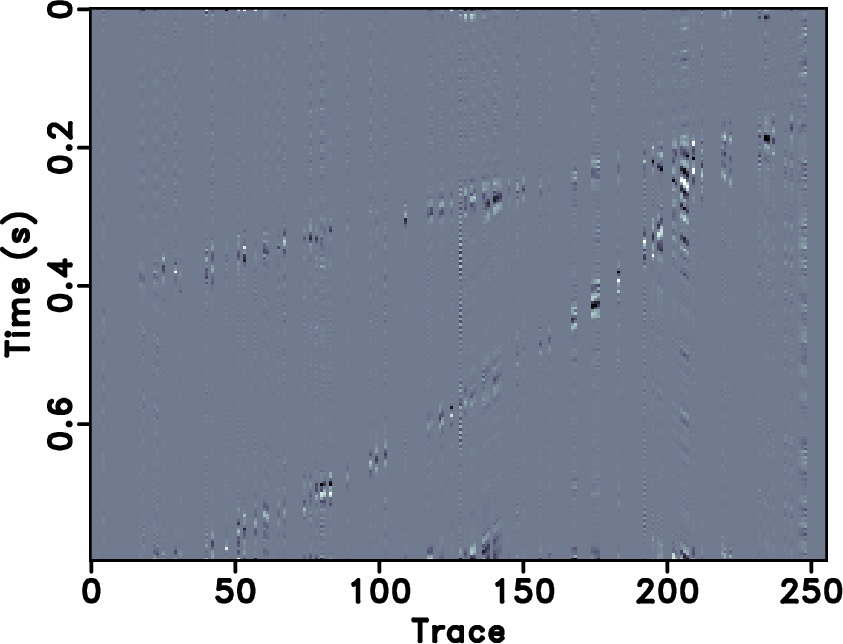
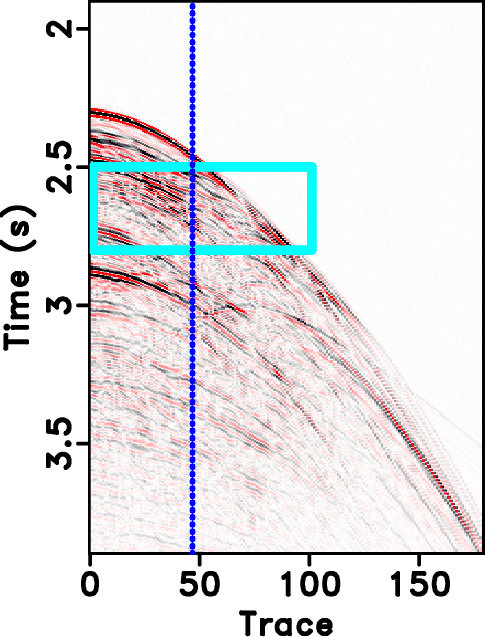
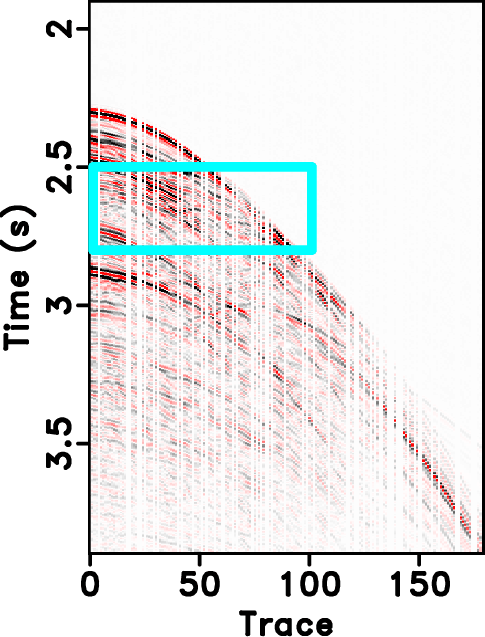
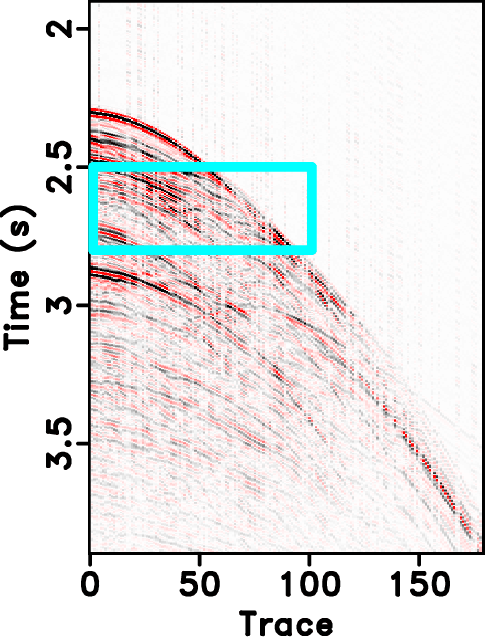
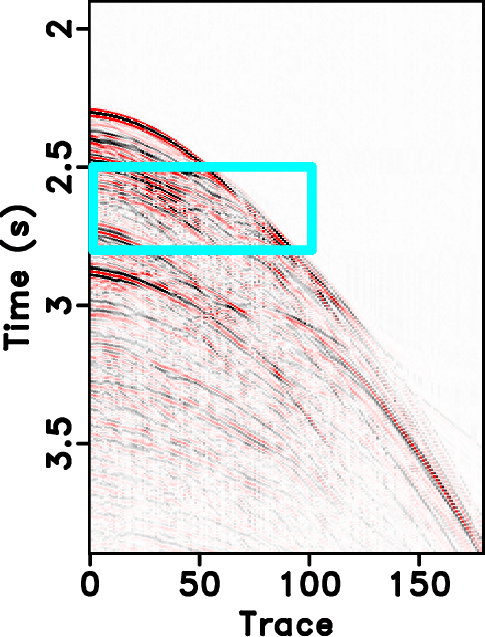
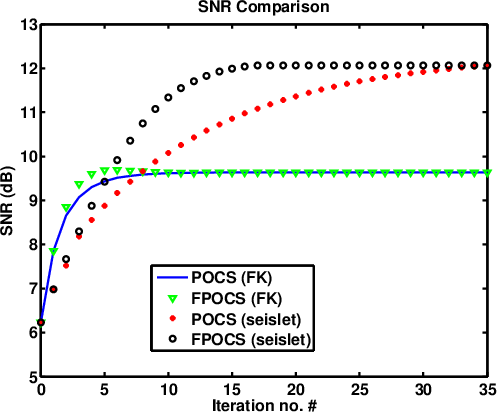
The second example is a field data example, as shown in Figures 13a. The incomplete data by randomly removing 30% traces is shown in Figure 13b. The reconstructed results for the field data example are shown in Figures 14. For the field data example, 18 % coefficients are preserved during the iterations. The error sections using different approaches are shown in Figure 16. It is obvious that the reconstructed data using seislet based approach are much more coherent than ![]() based and have less reconstruction error. We also show zoomed sections in Figure 18 for better comparison. The SNR diagrams are shown in Figure 19. It also shows a similar conclusion that is consistent with that from the previous synthetic example: the seislet-based approaches can obtain better reconstruction performance and the the FPOCS can obtain much faster convergence. Because
based and have less reconstruction error. We also show zoomed sections in Figure 18 for better comparison. The SNR diagrams are shown in Figure 19. It also shows a similar conclusion that is consistent with that from the previous synthetic example: the seislet-based approaches can obtain better reconstruction performance and the the FPOCS can obtain much faster convergence. Because ![]() transform is a global transform,
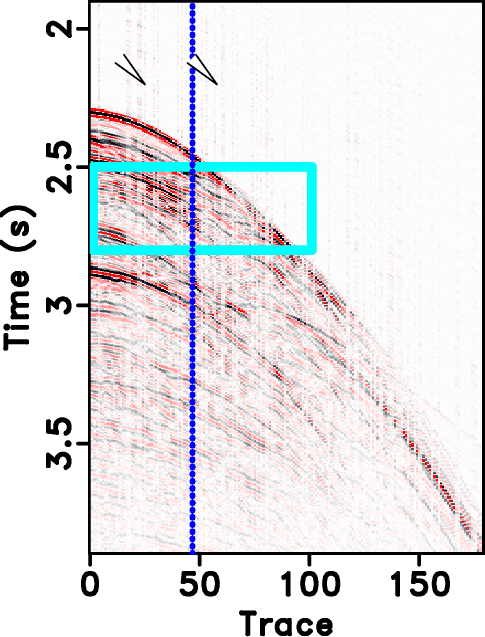
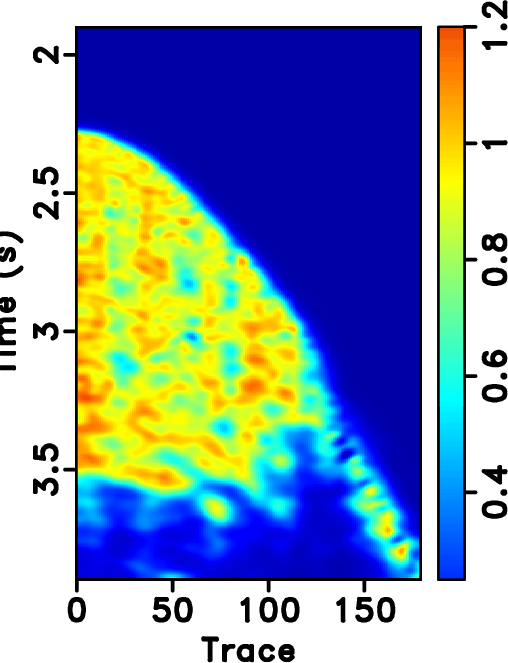
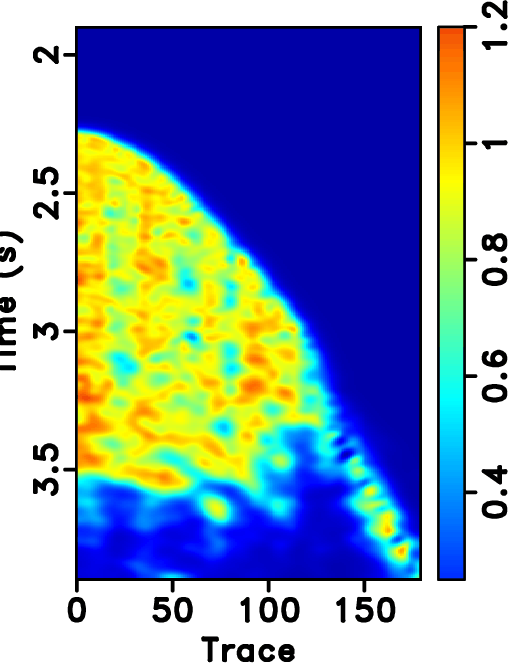
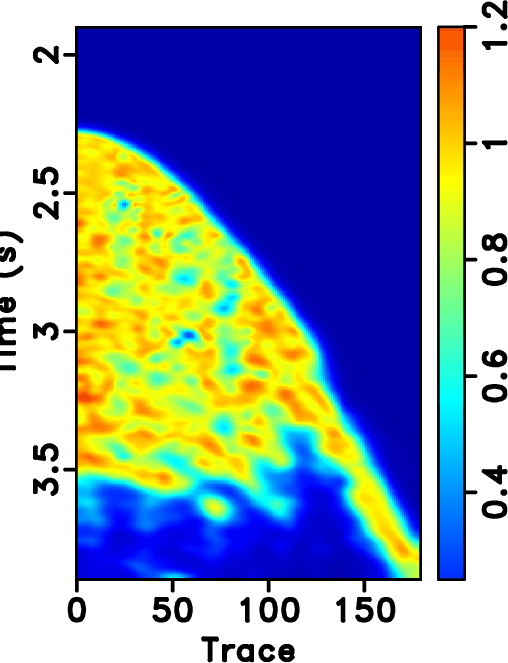
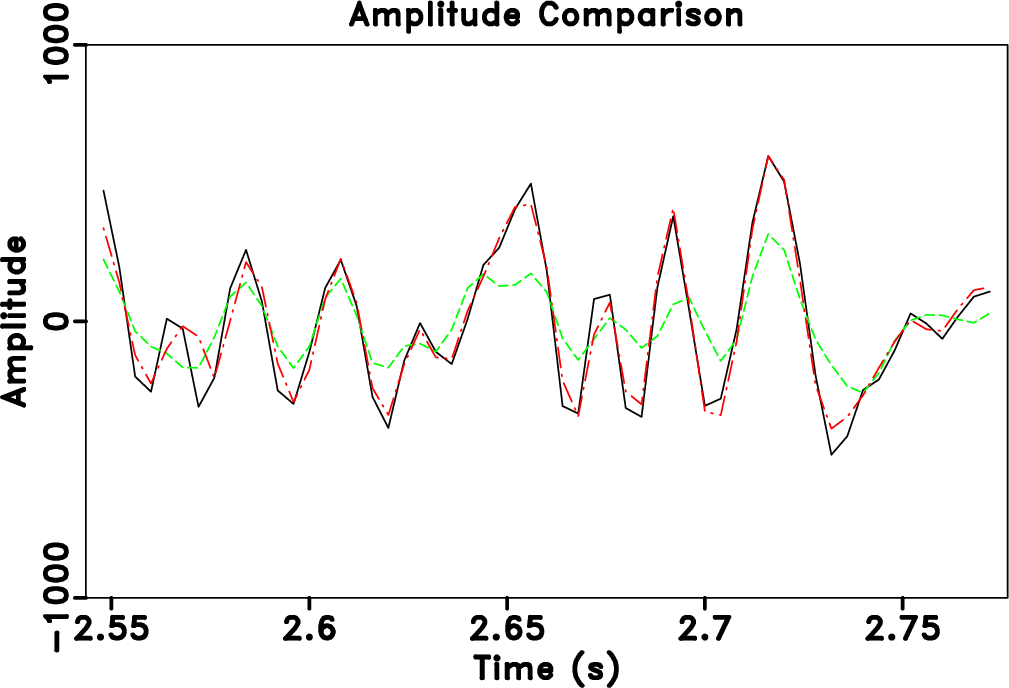
transform is a global transform, ![]() based approaches will cause artifacts outside the main data structure, as can be seen at the top of Figure 14b. Since the seislet transform is a local transform, it will not cause such artifacts. Figure 20a shows the amplitude comparison for the 48th trace (as highlighted in Figures 13a, 14b and 14d). It is obvious that the seislet based FPOCS has less reconstruction error compared with the
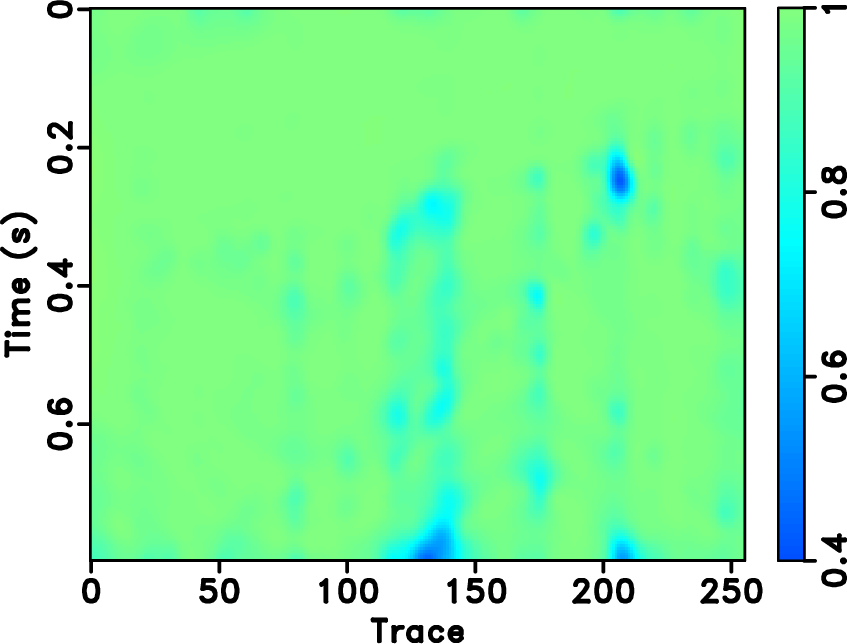
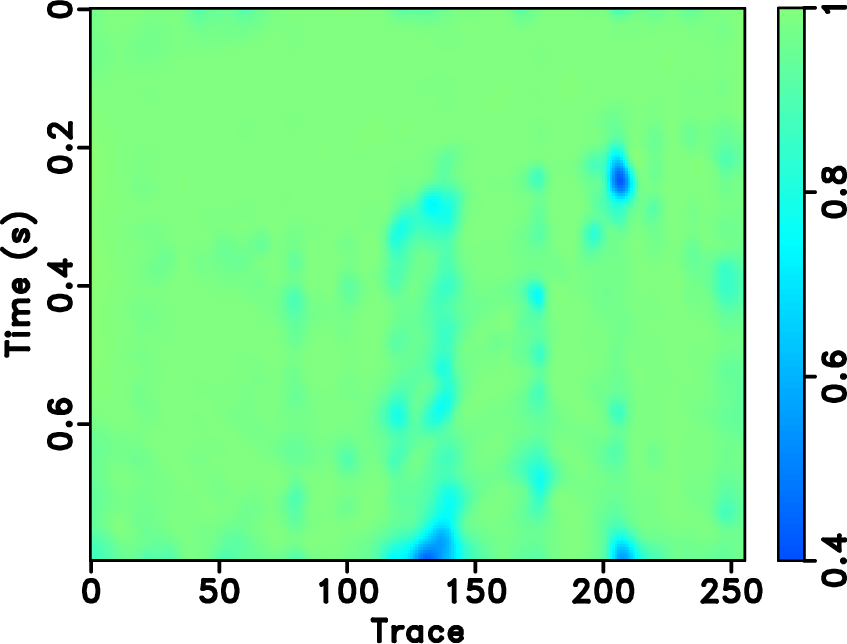
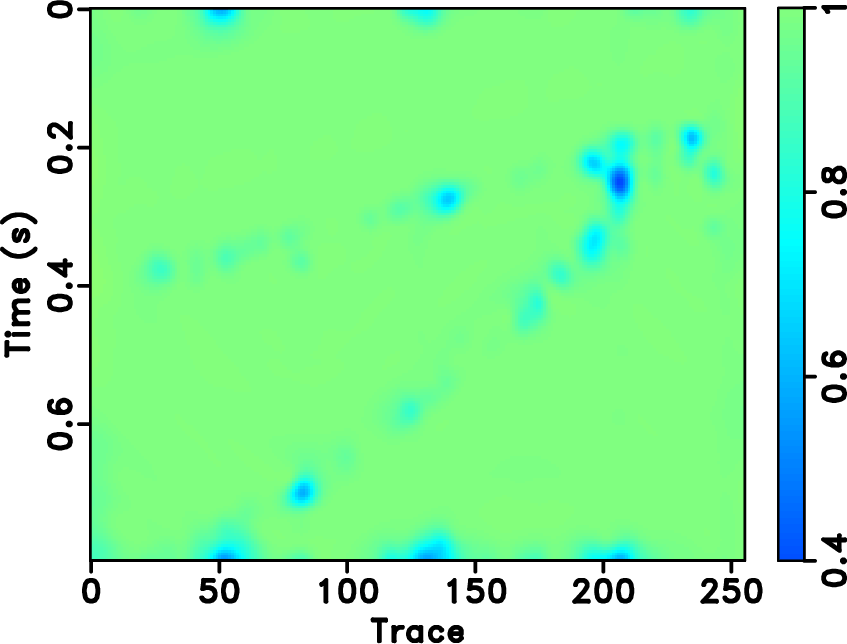
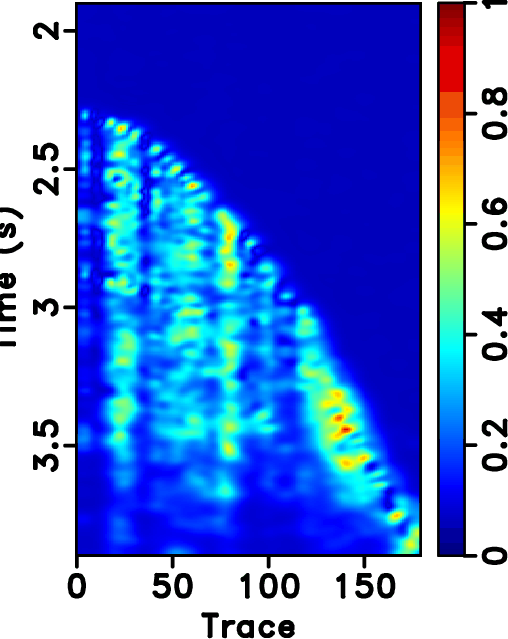
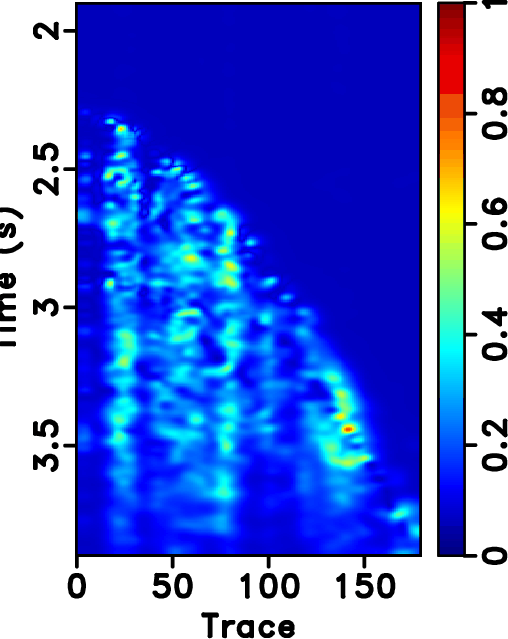
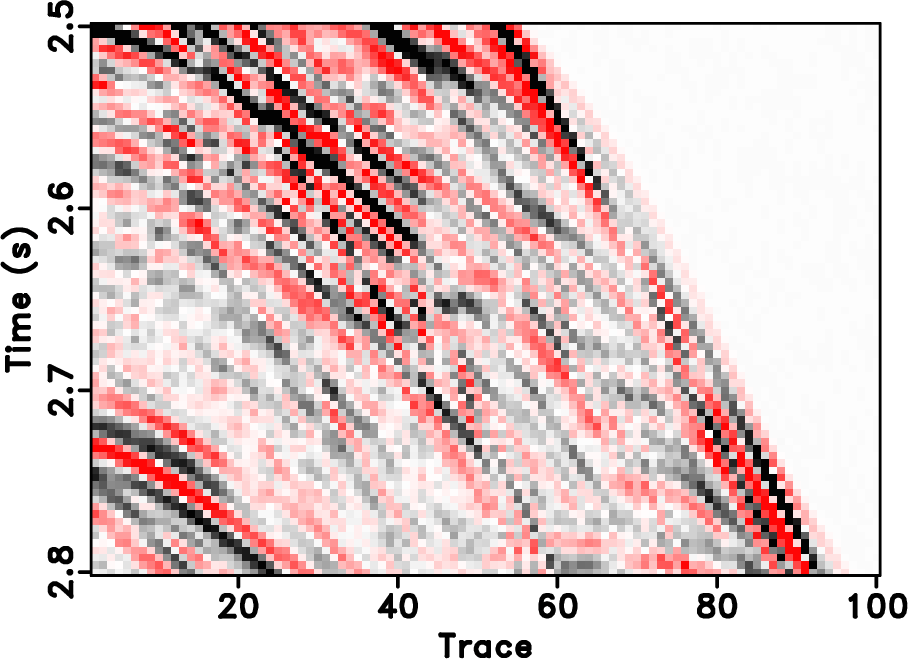
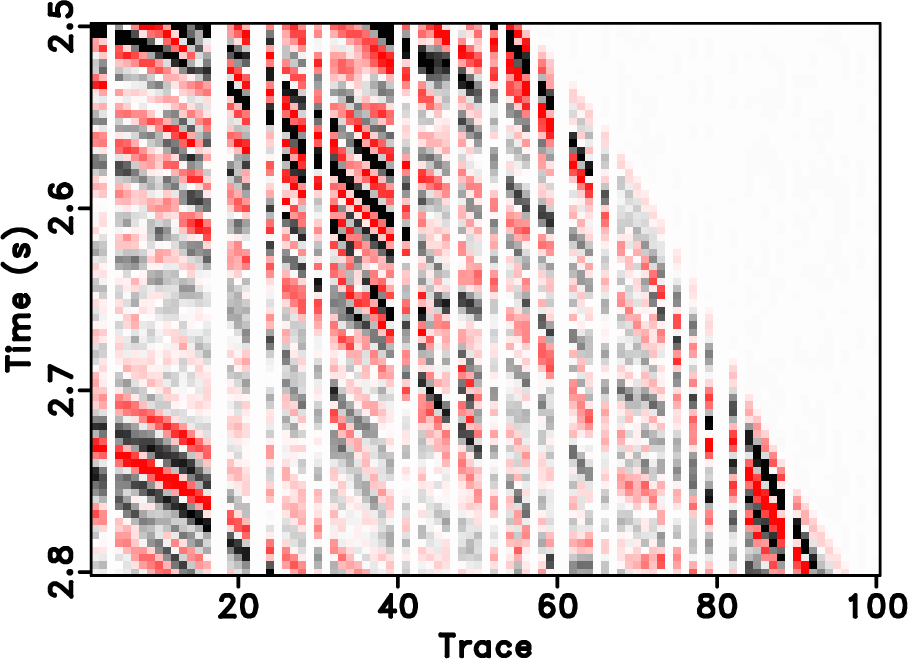
based approaches will cause artifacts outside the main data structure, as can be seen at the top of Figure 14b. Since the seislet transform is a local transform, it will not cause such artifacts. Figure 20a shows the amplitude comparison for the 48th trace (as highlighted in Figures 13a, 14b and 14d). It is obvious that the seislet based FPOCS has less reconstruction error compared with the ![]() based FPOCS. Figure 15 shows the local similarity between the true field data and the reconstructed datasets. The two similarity maps on the bottom row have relatively smaller values than that on the top row, indicating that the seislet based approaches can obtain more accurate reconstructed results. The low-value anomalies in the deep-water part are caused by the low-amplitude (nearly zero) deep-water reflections and should not be taken into the consideration in evaluating different performance. Figure 17 shows the local similarity between the true dataset and the reconstruction error. The two similarity maps on the bottom show small values while the two maps on the top row show high-value anomalies, further confirming the superior performance using the seislet-based approach. Figure 20b shows the local similarity comparison for the field data example (between the reconstructed trace and the true trace), which further confirms the aforementioned conclusions.
based FPOCS. Figure 15 shows the local similarity between the true field data and the reconstructed datasets. The two similarity maps on the bottom row have relatively smaller values than that on the top row, indicating that the seislet based approaches can obtain more accurate reconstructed results. The low-value anomalies in the deep-water part are caused by the low-amplitude (nearly zero) deep-water reflections and should not be taken into the consideration in evaluating different performance. Figure 17 shows the local similarity between the true dataset and the reconstruction error. The two similarity maps on the bottom show small values while the two maps on the top row show high-value anomalies, further confirming the superior performance using the seislet-based approach. Figure 20b shows the local similarity comparison for the field data example (between the reconstructed trace and the true trace), which further confirms the aforementioned conclusions.
|
|---|
|
sigmoid-1,sigmoid-zero-0
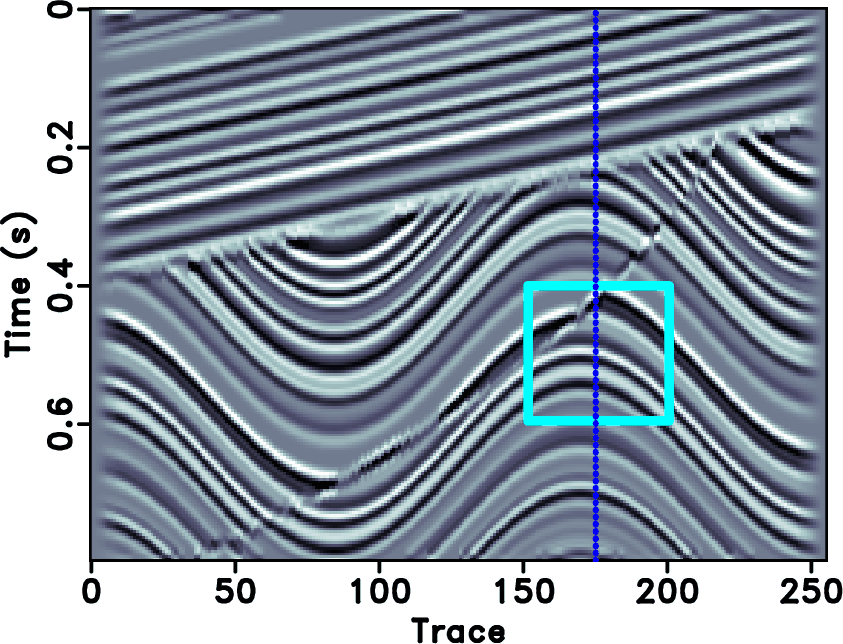
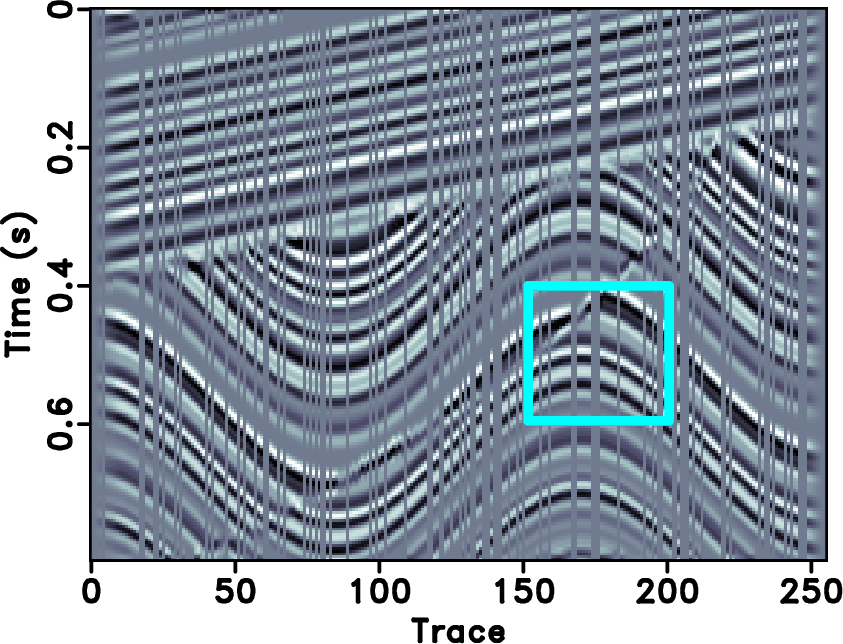
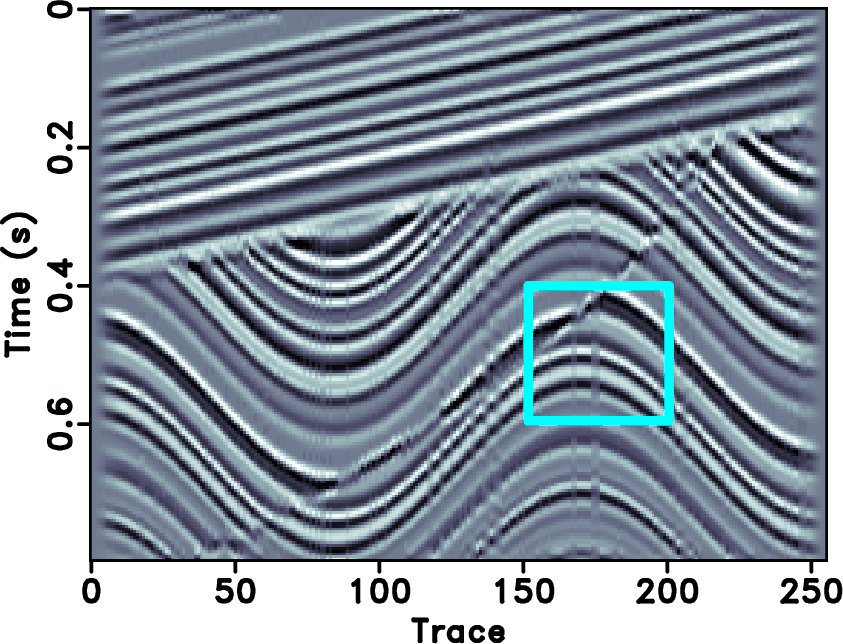
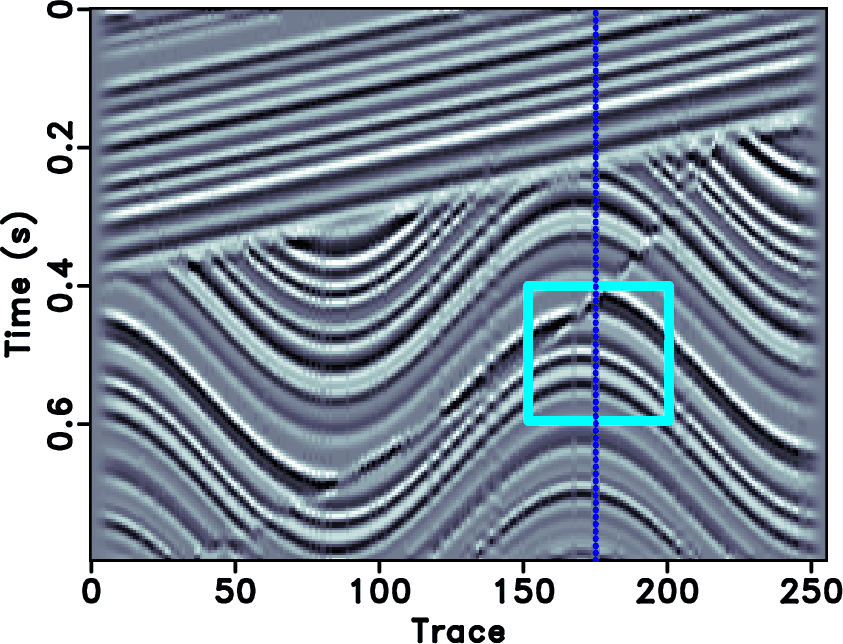
Figure 3. (a) Synthetic data. (b) Decimated synthetic data with 30% removed traces. |
|
|

|
|---|
|
data-pocs-fft-0,data-fpocs-fft-1,data-pocs-seis-0,data-fpocs-seis-1
Figure 4. (a)-(d) Reconstructed sections corresponding to POCS with |
|
|

|
|---|
|
simi-pocs-fft,simi-fpocs-fft,simi-pocs-seis,simi-fpocs-seis
Figure 5. Local similarity between the reconstructed sections with the true data using different approaches. (a) |
|
|
|
|---|
|
diff-pocs-fft,diff-fpocs-fft,diff-pocs-seis,diff-fpocs-seis
Figure 6. (a)-(d) Reconstruction error sections corresponding to Figures 4a-4d, respectively. |
|
|


|
|---|
|
simi-diff-pocs-fft,simi-diff-fpocs-fft,simi-diff-pocs-seis,simi-diff-fpocs-seis
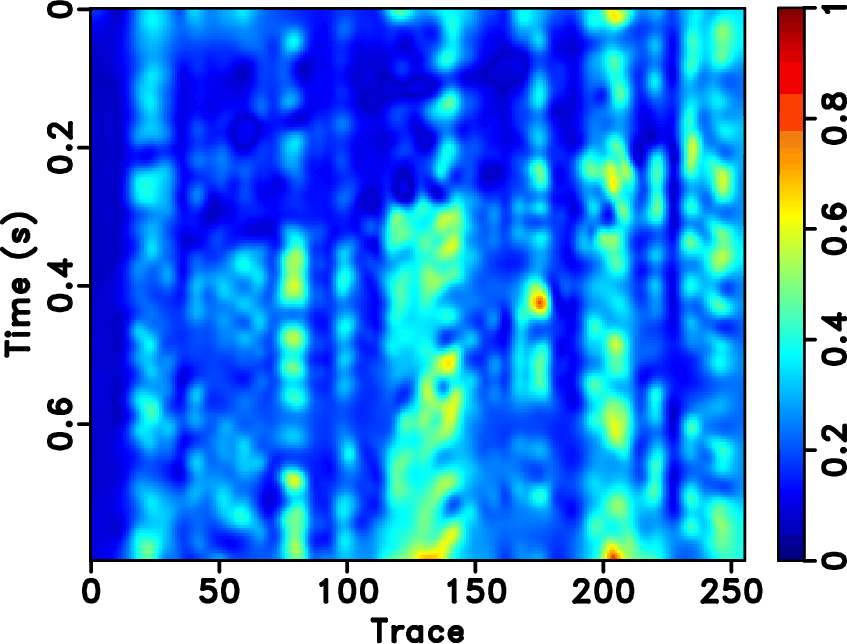
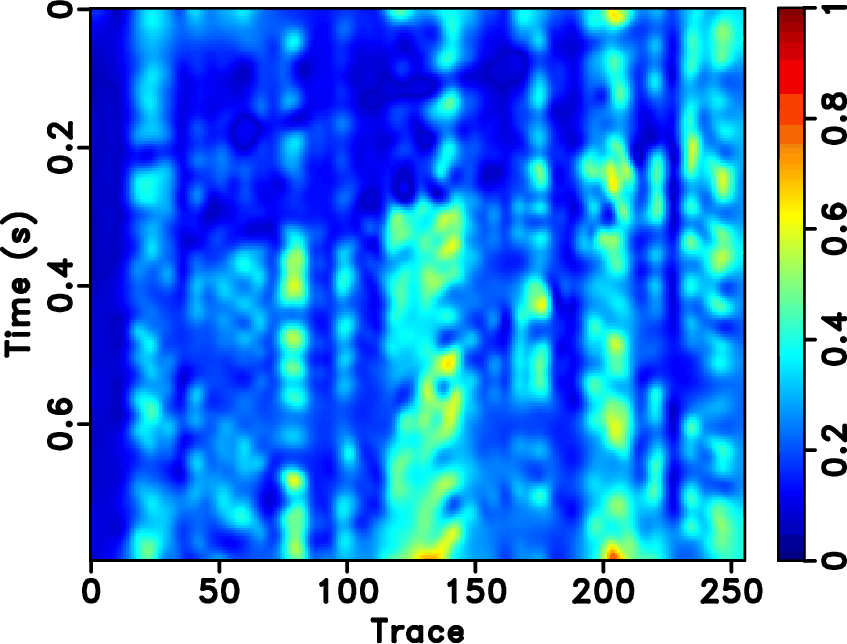
Figure 7. Local similarity between the error sections with the true data using different approaches. (a) |
|
|
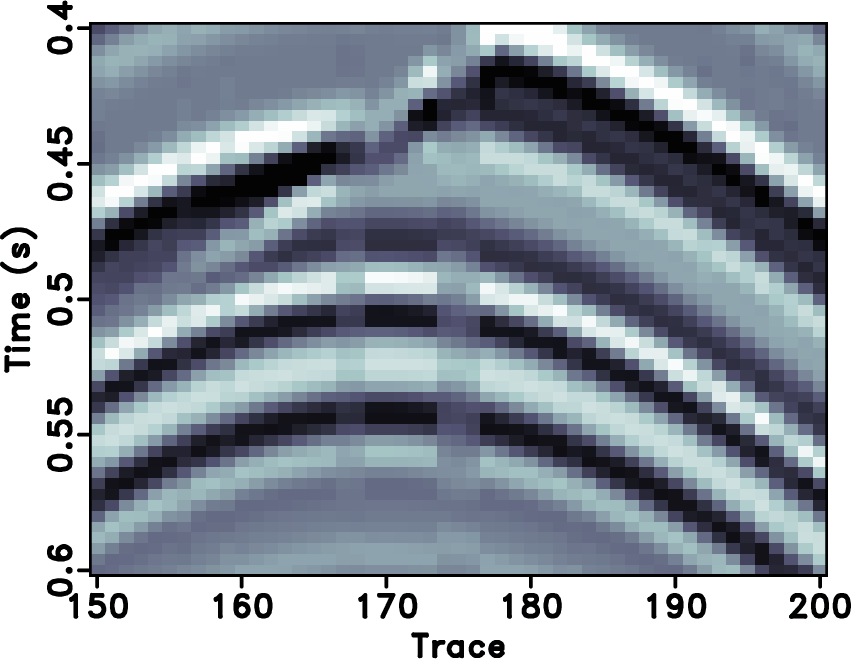
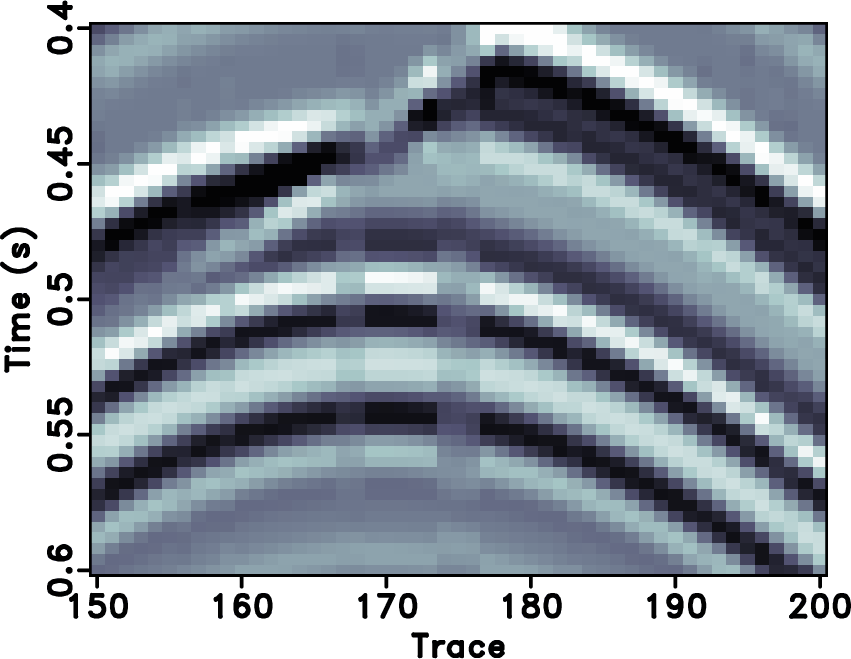
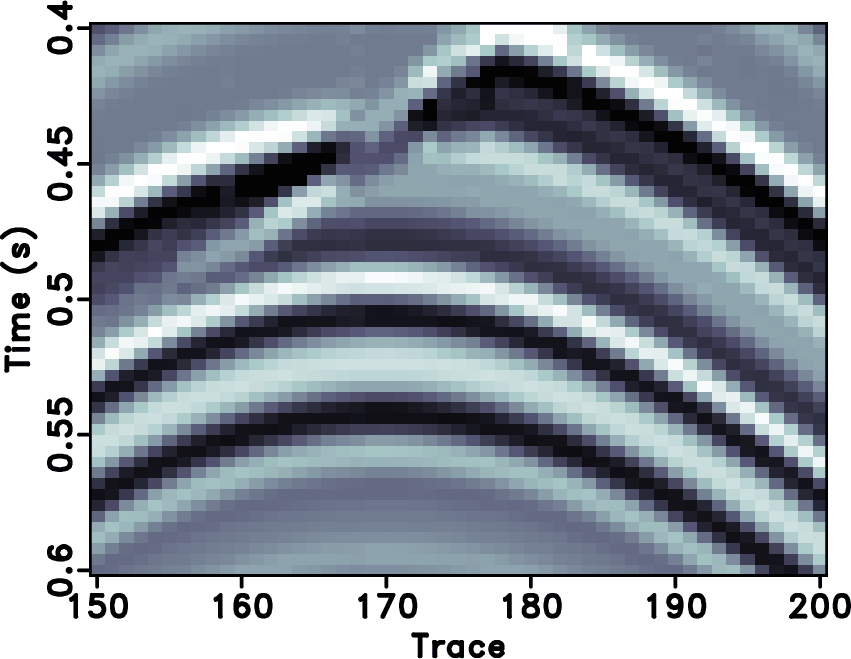
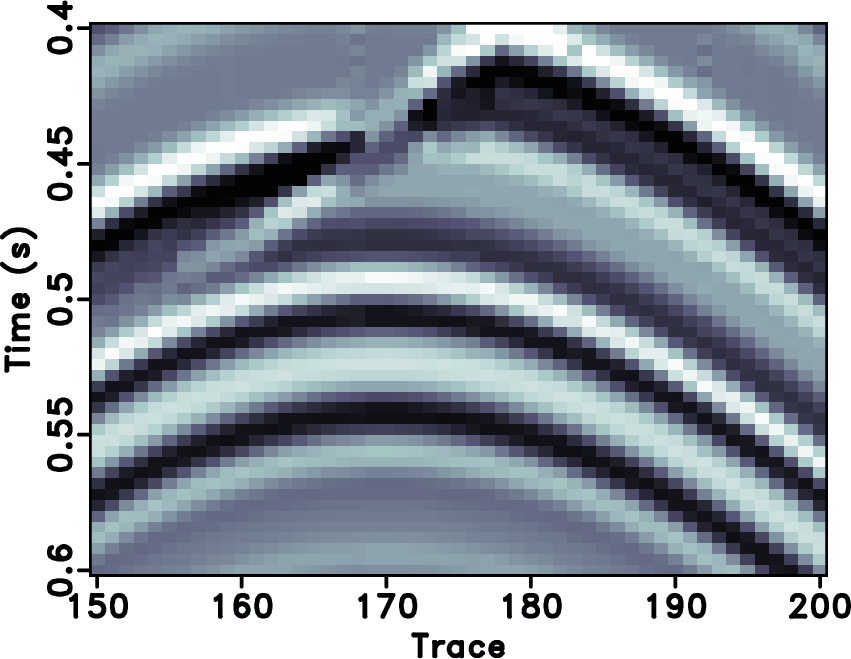
|
|---|
|
data-z,data-zero-z,data-pocs-fft-z,data-fpocs-fft-z,data-pocs-seis-z,data-fpocs-seis-z
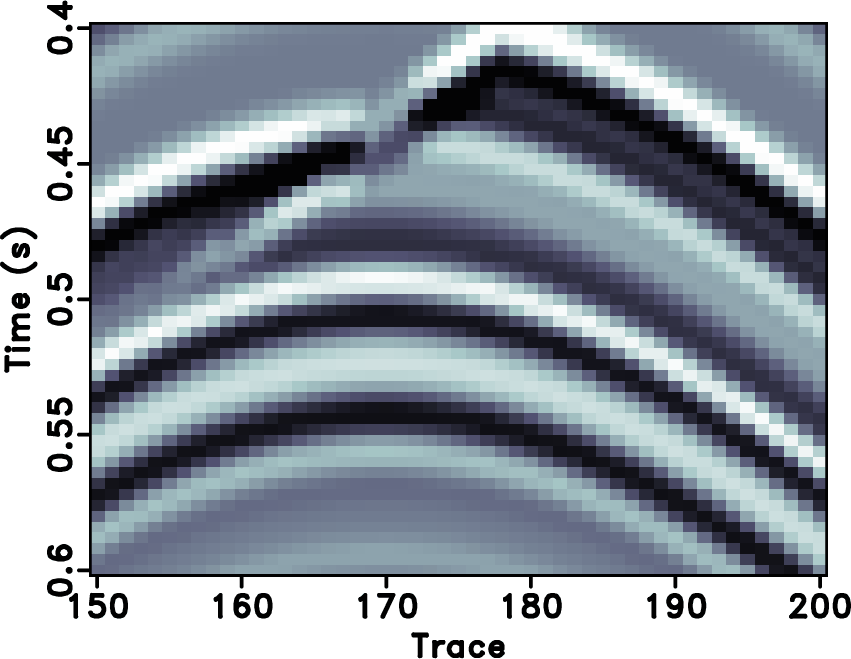
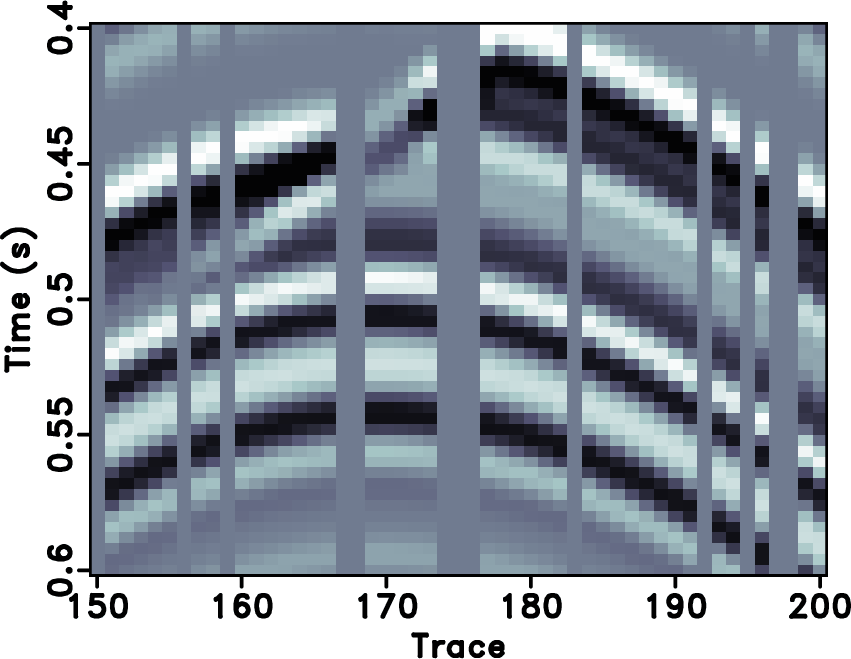
Figure 8. Zoomed sections. (a) True data. (b) Decimated data. (c) POCS with |
|
|
|
|---|
|
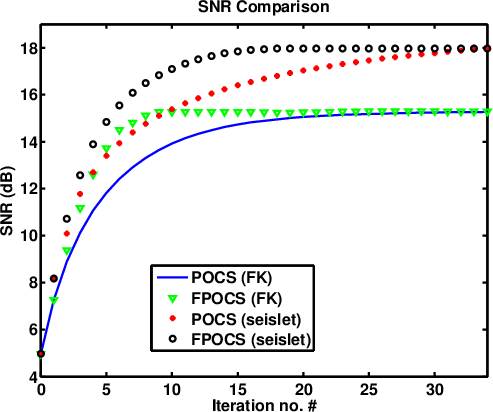
snrs
Figure 9. SNR comparison of the synthetic example, when the best parameter is selected. |
|
|
|
|---|
|
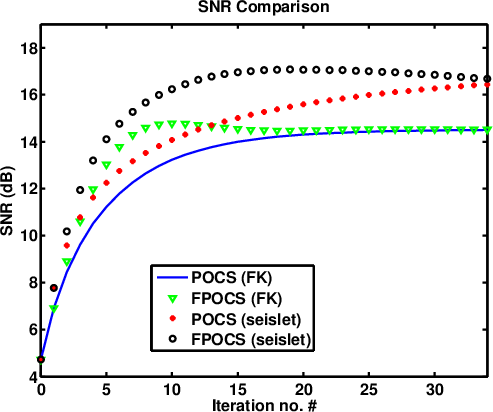
snrs0
Figure 10. SNR comparison of the synthetic example, when the inappropriate parameter is selected. |
|
|
|
|---|
|
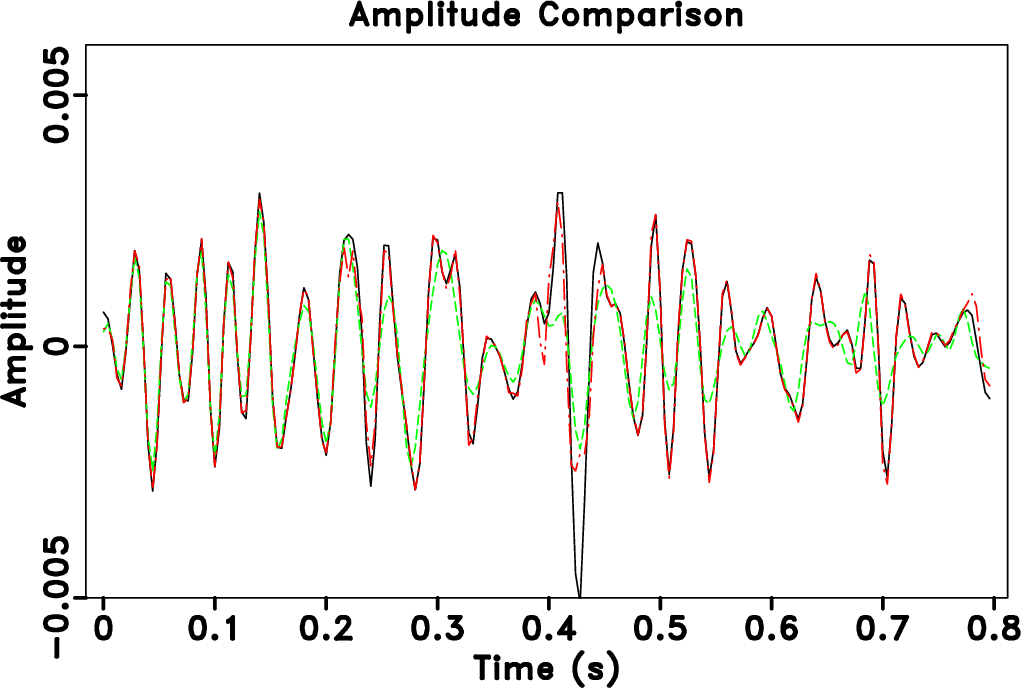
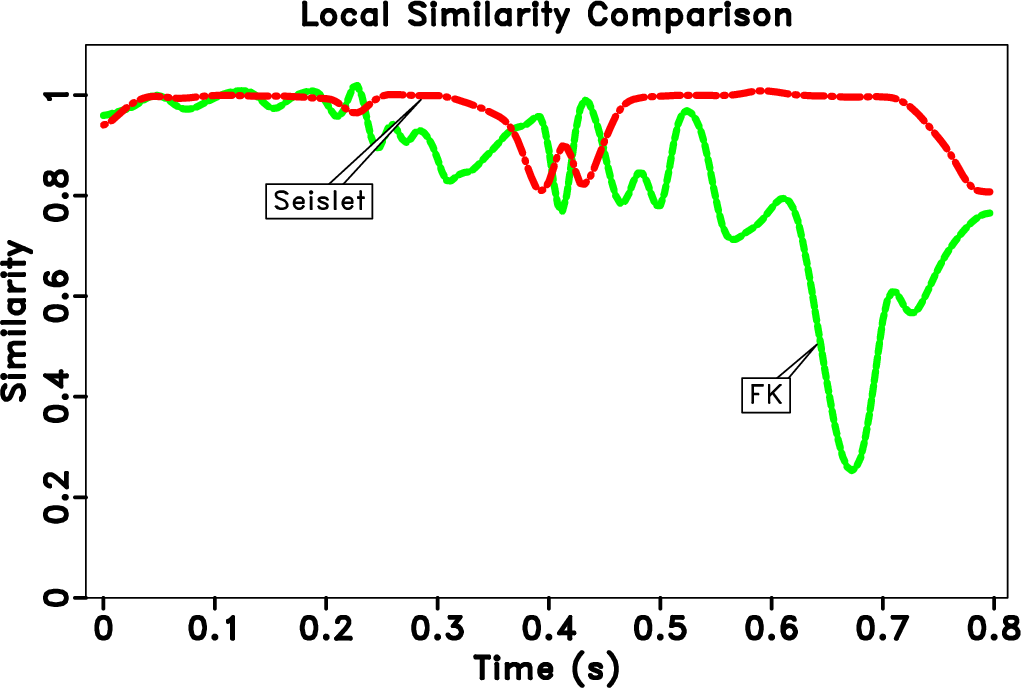
trace-comp,tsimi-comp
Figure 11. (a) Amplitude comparison. (b) Local similarity comparison. Black solid line denotes the true trace. Red dot dashed line denotes FPOCS with seislet thresholding. Green dashed line denotes FPOCS using |
|
|
|
|---|
|
sigmoid-zero,istpocs-snrs,sigmoidn-zero,istpocsnoise-snrs
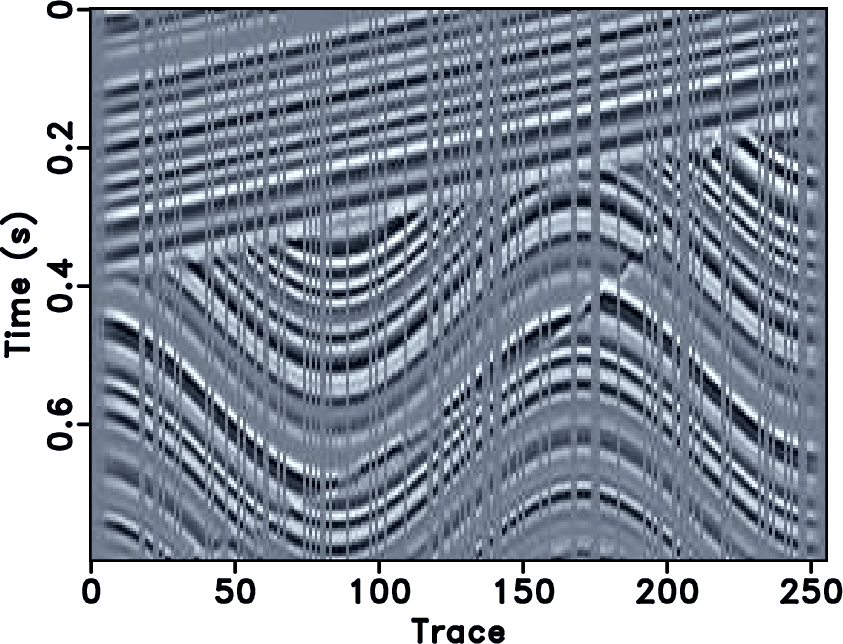
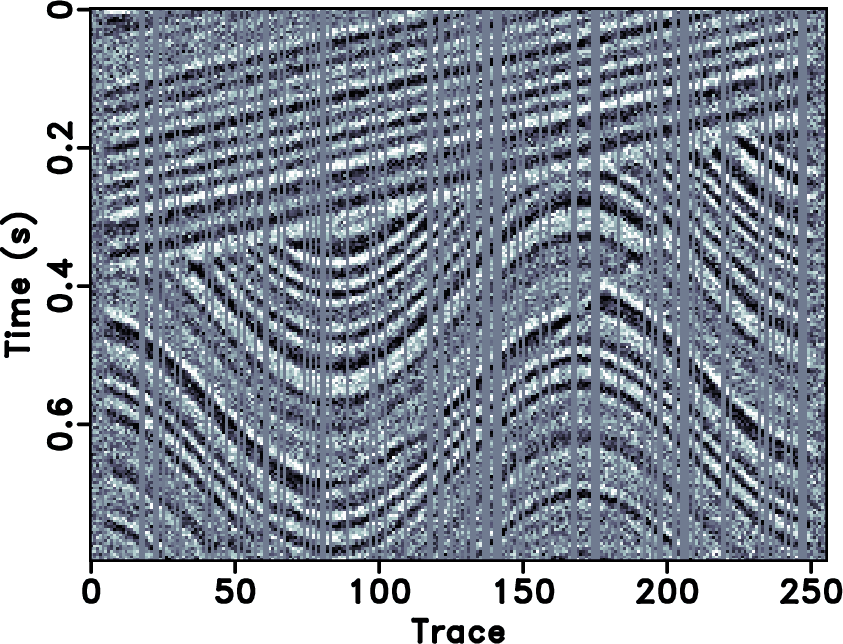
Figure 12. (a) Clean synthetic data. (b) Comparison of POCS (FPOCS) and IST (FISTA) of clean data in terms of SNR. (c) Noisy synthetic data. (d) Comparison of POCS (FPOCS) and IST (FISTA) of noisy data in terms of SNR. |
|
|
|
|---|
|
sean-1,sean-zero-0
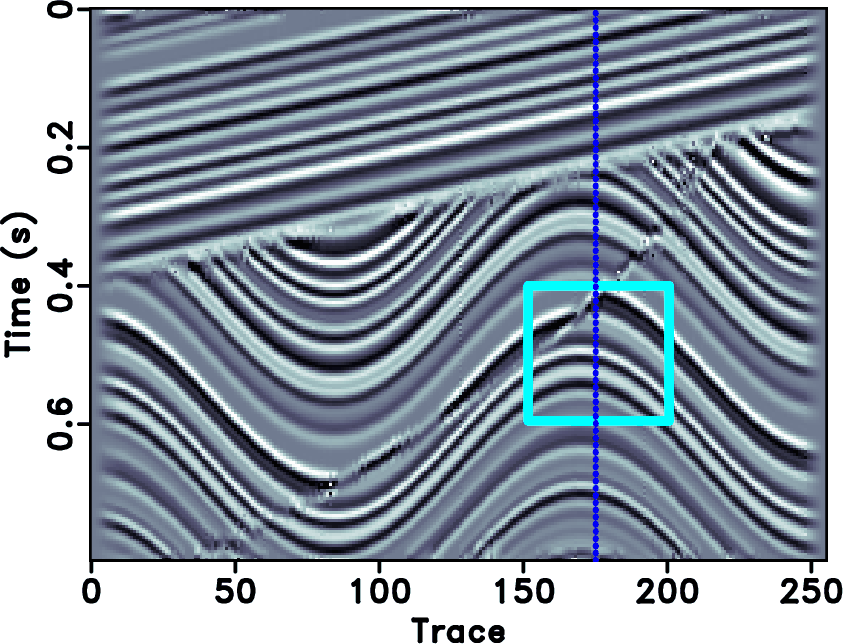
Figure 13. Field data example. (a)True field data. (b) Decimated field data with 30 % removed traces. |
|
|

|
|---|
|
sean-pocs-fft-0,sean-fpocs-fft-1,sean-pocs-seis-0,sean-fpocs-seis-1
Figure 14. Field data example. (a)-(d) Reconstructed sections corresponding to POCS with |
|
|
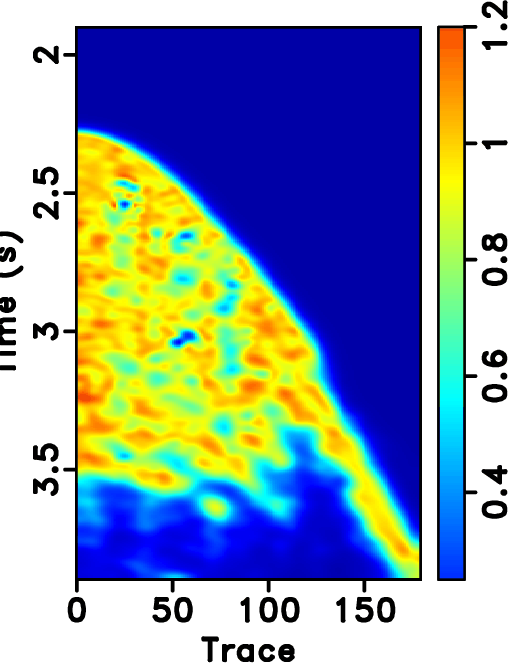
|
|---|
|
sean-simi-pocs-fft,sean-simi-fpocs-fft,sean-simi-pocs-seis,sean-simi-fpocs-seis
Figure 15. Field data example. Local similarity between the reconstructed sections with the true data using different approaches. (a) |
|
|

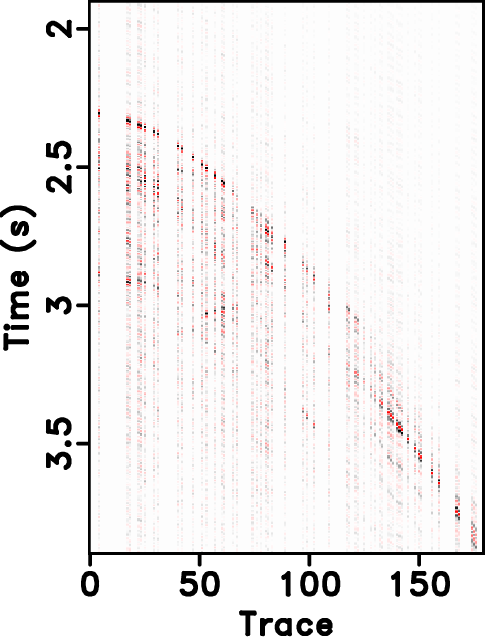
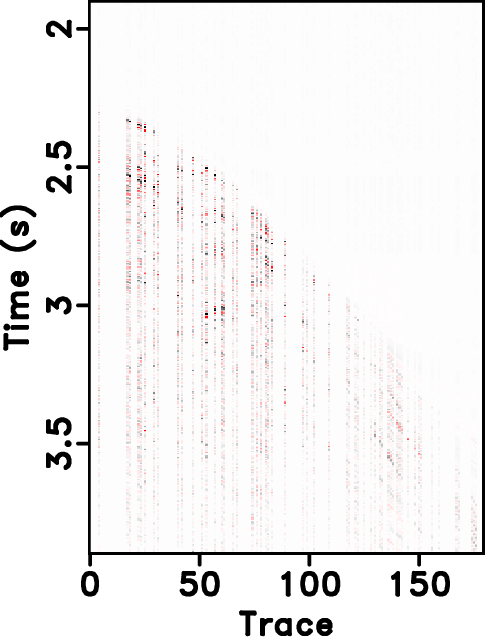
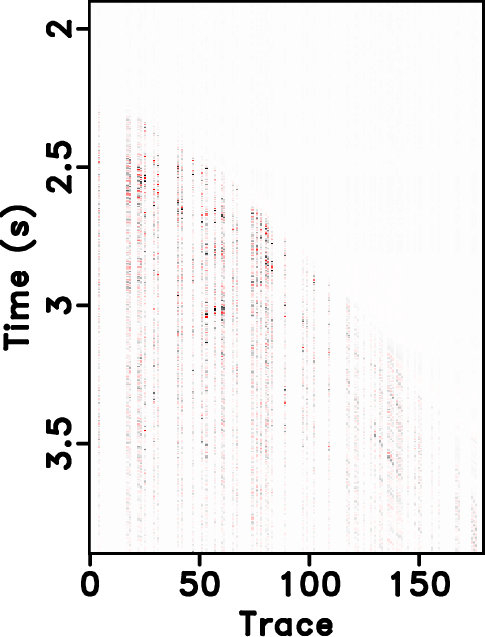
|
|---|
|
sean-diff-pocs-fft,sean-diff-fpocs-fft,sean-diff-pocs-seis,sean-diff-fpocs-seis
Figure 16. Field data example. (a)-(d) Reconstruction error sections corresponding to Figures 14a-14d, respectively. |
|
|


|
|---|
|
sean-simi-diff-pocs-fft,sean-simi-diff-fpocs-fft,sean-simi-diff-pocs-seis,sean-simi-diff-fpocs-seis
Figure 17. Field data example. Local similarity between the error sections with the true data using different approaches. (a) |
|
|
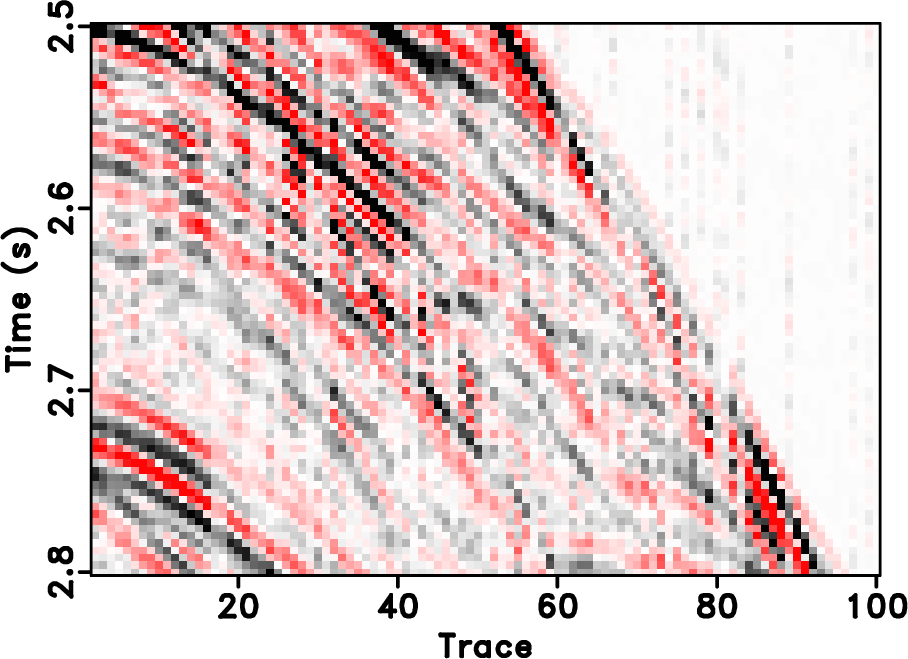
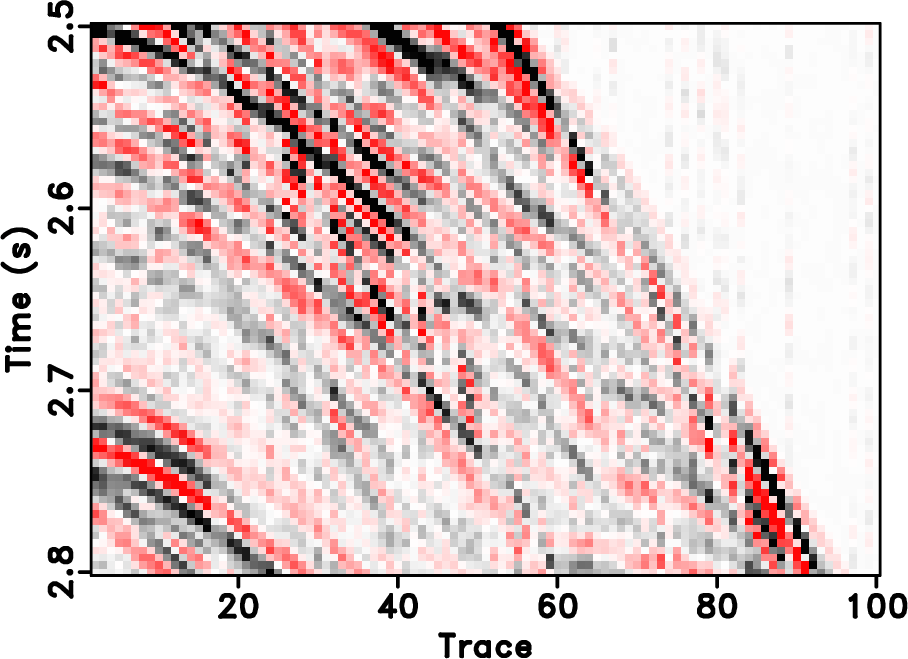
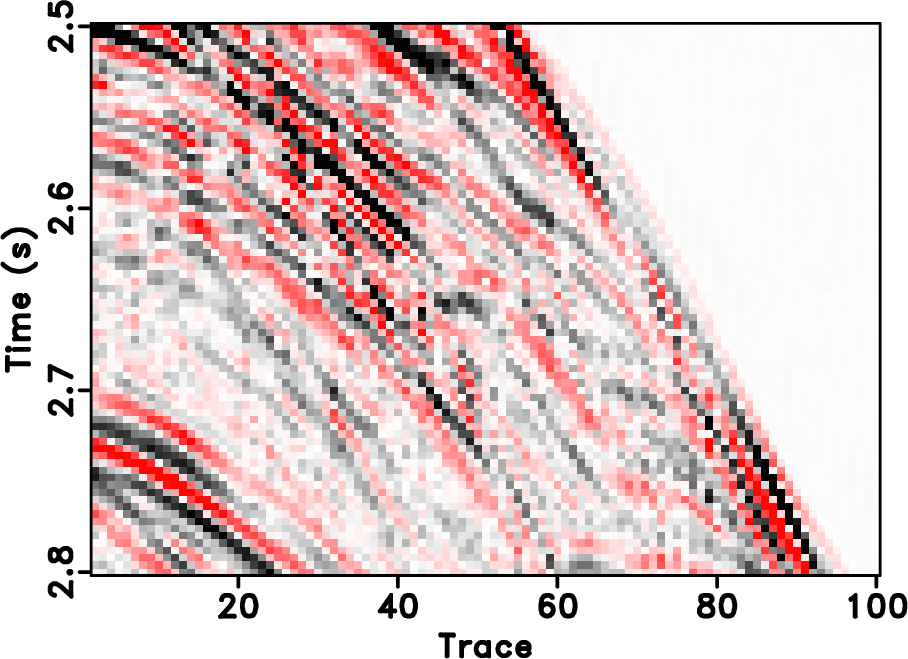
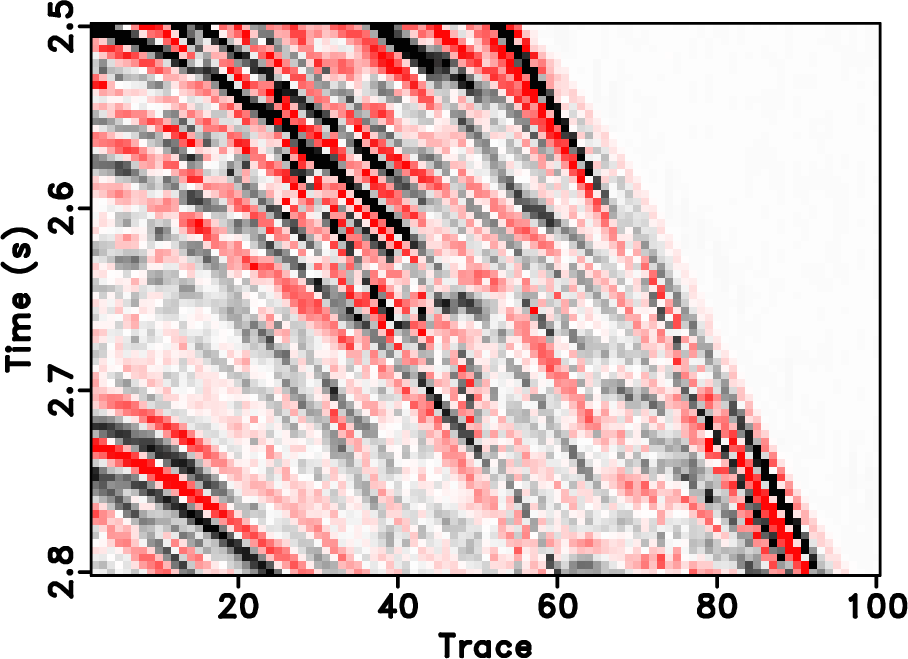
|
|---|
|
sean-z,sean-zero-z,sean-pocs-fft-z,sean-fpocs-fft-z,sean-pocs-seis-z,sean-fpocs-seis-z
Figure 18. Zoomed sections of the field data example. (a) True data. (b) Decimated data. (c) POCS with |
|
|
|
|---|
|
sean-snrs
Figure 19. SNR comparison of the field data example. |
|
|

|
|---|
|
sean-trace-comp,sean-tsimi-comp
Figure 20. Field data example. (a) Amplitude comparison. (b) Local similarity comparison. Black solid line denotes the true trace. Red dot dashed line denotes FPOCS with seislet thresholding. Green dashed line denotes FPOCS using |
|
|