 |
 |
 |
 | Iterative deblending of simultaneous-source seismic data using seislet-domain shaping regularization |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Chen et al.: Deblending
Previous: Acknowledgments
-
Abma, R., Q. Zhang, A. Arogunmati, and G. Beaudoin, 2012, An overview of
BP's marine independent simultaneous source field trials: 82nd Annual
International Meeting, SEG, Expanded Abstracts, 1404.1.
-
-
Abma, R. L., T. Manning, M. Tanis, J. Yu, and M. Foster, 2010, High quality
separation of simultaneous sources by sparse inversion: 72nd Annual
International Conference and Exhibition, EAGE, Extended Abstracts.
-
-
Beasley, C. J., B. Dragoset, and A. Salama, 2012, A 3d simultaneous source
field test processed using alternating projections: a new active separation
method: Geophysical Prospecting, 60, 591-601.
-
-
Berkhout, A. J., 2008, Changing the mindset in seismic data acquisition: The
Leading Edge, 27, 924-938.
-
-
Berkhout, A. J., D. J. Verschuur, and G. Blacquière, 2012, illumination
properties and imaging promises of blended, multiple-scattering seismic data:
a tutorial: Geophysical Prospecting, 60, 713-732.
-
-
Canales, L., 1984, Random noise reduction: SEG expanded abstracts: 54th Annual
international meeting, 525-527.
-
-
Candès, E. J., and Y. Plan, 2010, A probabilistic and ripless theory of
compressed sensing: IEEE Transactions on Information Theory, 57,
7235-7254.
-
-
Chen, Y., and J. Ma, 2014, Random noise attenuation by f-x empirical
mode decomposition predictive filtering: Geophysics, 79, V81-V91.
-
-
Choi, Y., and T. Alkhalifah, 2012, Application of multi-source waveform
inversion to marine streamer data using the global correlation norm:
Geophysical Prospecting, 60, 748-758.
-
-
Cohen, A., I. Daubechies, and J. C. Feauveau, 1992, Biorthogonal bases of
compactly supported wavelets: Communications on Pure and Applied Mathematics,
45, 485-560.
-
-
Daubechies, I., M. Defrise, and C. D. Mol, 2004, An iterative thresholding
algorithm for linear inverse problems with a sparsity constraint:
Communications on Pure and Applied Mathematics, 57, 1413-1457.
-
-
Daubechies, I., M. Fornasier, and I. Loris, 2008, Accelerated projected
gradient method for linear inverse problems with sparsity constraints:
Journal of Fourier Analysis and Applications, 14, 764-792.
-
-
Donoho, D. L., 1995, De-noising by soft-thresholding: IEEE transactions on
information theory, 41, 613-627.
-
-
Donoho, D. L., and I. M. Johnstone, 1994, Ideal spatial adaptation by wavelet
shrinkage: Biometrika, 81, 425-455.
-
-
Doulgeris, P., and K. Bube, 2012, Analysis of a coherency-constrained
inversion for the separation of blended data: discovering the leakage
subspace: 74th Annual International Conference and Exhibition, EAGE, Extended
Abstracts.
-
-
Doulgeris, P., K. Bube, G. Hampson, and G. Blacquiere, 2012, Covergence
analysis of a coherency-constrained inversion for the separation of blended
data: Geophysical Prospecting, 60, 769-781.
-
-
Fomel, S., 2002, Application of plane-wave destruction filters: Geophysics,
67, 1946-1960.
-
-
----, 2006, Towards the seislet transform: 76th Annual International
Meeting, SEG, Expanded Abstracts, 2847-2850.
-
-
----, 2007, Shaping regularization in geophysical-estimation problems:
Geophysics, 72, R29-R36.
-
-
----, 2008, Nonlinear shapping regularization in geophysical inverse
problems: 78th Annual International Meeting, SEG, Expanded Abstracts,
2046-2051.
-
-
Fomel, S., and Y. Liu, 2010, Seislet transform and seislet frame: Geophysics,
75, V25-V38.
-
-
Galbraith, M., and Z. Yao, 2012, Fx plus deconvolution for seismic data noise
reduction: 82nd Annual International Meeting, SEG, Expanded Abstracts, 1-4.
-
-
Gao, J., X. Chen, G. Liu, and J. Ma, 2010, Irregular seismic data
reconstruction based on exponentional threshold model of pocs method: Applied
Geophysics, 7, 229-238.
-
-
Guitton, A., and E. Diaz, 2012, Attenuating crosstalk noise with simultaneous
source full waveform inversion: Geophysical Prospecting, 60, 759-768.
-
-
Hampson, G., J. Stefani, and F. Herkenhoff, 2008, Acquisition using
simultaneous sources: The Leading Edge, 27, 918-923.
-
-
Hennenfent, G., and F. Herrmann, 2006, Seismic denoising with nonunformly
sampled curvelets: Computing in Science & Engineering, 8, 16-25.
-
-
Huo, S., Y. Luo, and P. G. Kelamis, 2012, Simultaneous sources separation via
multidirectional vector-median filtering: Geophysics, 77, V123-V131.
-
-
Liu, Y., 2013, Noise reduction by vector median filtering: Geophysics, 78, V79-V87.
-
-
Liu, Y., and S. Fomel, 2012, Seismic data analysis using local time-frequency
decomposition: Geophyscial Prospecting, 60, 1-10.
-
-
Liu, Y., S. Fomel, C. Liu, D. Wang, G. Liu, and X. Feng, 2009a, High-order
seislet transform and its application of random noise attenuation: Chinese
Journal of Geophysics, 52, 2142-2151.
-
-
Liu, Y., C. Liu, and D. Wang, 2009b, A 1d time-varying median filter for
seismic random, spike-like noise elimination: Geophysics, 74, V17-V24.
-
-
Mahdad, A., 2012, Deblending of seismic data: TU Delft, PhD thesis.
-
-
Mahdad, A., P. Doulgeris, and G. Blacquiere, 2011, Separation of blended data
by iterative estimation and subtraction of blending interference noise:
Geophysics, 76, Q9-Q17.
-
-
----, 2012, Iterative method for the separation of blended seismic data:
discussion on the algorithmic aspects: Geophysical Prospecting, 60,
782-801.
-
-
Mallat, S. G., 2009, A wavelet tour of signal processing: The sparse way:
Academic Press.
-
-
Mitchell, S., C. Ray, E. Marc, D. Hays, and K. Craft, 2010, Fairfieldnodal's
excellent nodal adventure: 80th Annual International Meeting, SEG, Expanded
Abstracts, 3740-3745.
-
-
Moore, I., B. Dragoset, T. Ommundsen, D. Wilson, C. Ward, and D. Eke, 2008,
Simultaneous source separation using dithered sources: 78th Annual
International Meeting, SEG, Expanded Abstracts, 2806-2809.
-
-
Naghizadeh, M., and M. D. Sacchi, 2010, Beyond alias hierarchical scale
curvelet interpolation of regularly and irregularly sampled seismic data:
Geophysics, 75, WB189-WB202.
-
-
Plessix, R.-E., G. Baeten, J. W. de Maag, F. ten Kroode, and Z. Rujie, 2012,
Full waveform inversion and distance separated simultaneous sweeping: a study
with a land seismic data set: Geophysical Prospecting, 60, 733-747.
-
-
Sacchi, M. D., and H. Kuehl, 2000, Fx arma filters: 70th Annual International
Meeting, SEG, Expanded Abstracts, 2092-2095.
-
-
Sweldens, W., 1995, Lifting scheme: A new philosophy in biorthogonal wavelet
constructions: Wavelet applications in signal and image processing iii:
Proceedings of SPIE 2569, 68-79.
-
-
van Borselen, R., R. Baardman, T. Martin, B. Goswami, and E. Fromyr, 2012, An
inversion approach to separating sources in marine simultaneous shooting
acquision-application to a gulf of mexico data set: Geophysical Prospecting,
60, 640-647.
-
-
Wang, D., C. Liu, Y. Liu, and G. Liu, 2008, Application of wavelet transform
based on lifting scheme and percentiles soft-threshold to elimination of
seismic random noise: Progress in Geophysics (in Chinese), 23,
1124-1130.
-
-
Wapenaar, K., J. van der Neut, and J. Thorbecke, 2012, Deblending by direct
inversion: Geophysics, 77, A9-A12.
-
-
Xue, Z., Y. Chen, S. Fomel, and J. Sun, 2014, Imaging incomplete data and
simultaneous-source data using least-squares reverse-time migration with
shaping regularization: 84th Annual International Meeting, SEG, Expanded
Abstracts, submitted.
-
-
Yang, P., J. Gao, and W. Chen, 2012, Improved pocs interpolation using a
percentage thresholding strategy and excessively zero-padded fft: 82nd Annual
International Meeting, SEG, Expanded Abstracts, 1-6.
-
-
----, 2013, On analysis-based two-step interpolation methods for randomly
sampled seismic data: Computers & Geosciences, 51, 449-461.
-
Appendix
A
Review of seislet transform
Fomel (2006) and Fomel and Liu (2010) proposed a digital wavelet-like transform, which is defined with the help of the wavelet-lifting scheme (Sweldens, 1995) combined with local plane-wave destruction. The wavelet-lifting utilizes predictability of even traces from odd traces of 2-D seismic data and finds a difference
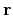 between them, which can be expressed as:
between them, which can be expressed as:
![$\displaystyle \mathbf{r}=\mathbf{o}-\mathbf{P\left[e\right]},$](img75.png) |
(19) |
where
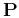 is the prediction operator.
A coarse approximation
is the prediction operator.
A coarse approximation
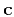 of the data can be achieved by updating the even component:
of the data can be achieved by updating the even component:
![$\displaystyle \mathbf{c}=\mathbf{e}+\mathbf{U\left[r\right]},$](img77.png) |
(20) |
where
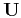 is the updating operator.
is the updating operator.
The digital wavelet transform can be inverted by reversing the lifting-scheme operations as follows:
![$\displaystyle \mathbf{e}=\mathbf{c}-\mathbf{U\left[r\right]},$](img79.png) |
(21) |
![$\displaystyle \mathbf{o}=\mathbf{r}+\mathbf{P\left[e\right]}.$](img80.png) |
(22) |
The foward transform starts with the finest scale (the original sampling) and goes to the coarsest scale. The inverse transfrom starts with the coarsest scale and goes back to the finest scale. At the start of forward transform,
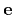 and
and
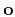 corresponds to the even and odd traces of the data domain. At the start of the inverse transform,
corresponds to the even and odd traces of the data domain. At the start of the inverse transform,
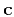 and
and
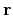 will have just one trace of the coarsest scale of the seislet domain.
will have just one trace of the coarsest scale of the seislet domain.
The above prediction and update operators can be defined, for example, as follows:
![$\displaystyle \mathbf{P}\left[\mathbf{e}\right]_k=\left(\mathbf{P}^{(+)}_k\left[\mathbf{e}_{k-1}\right]+\mathbf{P}^{(-)}_k\left[\mathbf{e}_k\right]\right)/2,$](img83.png) |
(23) |
and
![$\displaystyle \mathbf{U}\left[\mathbf{r}\right]_k=\left(\mathbf{P}^{(+)}_k\left[\mathbf{r}_{k-1}\right]+\mathbf{P}^{(-)}_k\left[\mathbf{r}_k\right]\right)/4,$](img84.png) |
(24) |
where
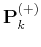 and
and
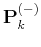 are operators that predict a trace from its left and right neighbors, correspondingly, by shifting seismic events according to their local slopes.
This scheme is analogous to CDF biorthogonal wavelets (Cohen et al., 1992). The predictions need to operate at different scales, which means different separation distances between traces. Taken through different scales, equations A-1-A-6 provide a simple definition for the 2D seislet transform. More accurate versions are based on other schemes for the digital wavelet transform (Liu et al., 2009a).
are operators that predict a trace from its left and right neighbors, correspondingly, by shifting seismic events according to their local slopes.
This scheme is analogous to CDF biorthogonal wavelets (Cohen et al., 1992). The predictions need to operate at different scales, which means different separation distances between traces. Taken through different scales, equations A-1-A-6 provide a simple definition for the 2D seislet transform. More accurate versions are based on other schemes for the digital wavelet transform (Liu et al., 2009a).
 |
 |
 |
 | Iterative deblending of simultaneous-source seismic data using seislet-domain shaping regularization |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Chen et al.: Deblending
Previous: Acknowledgments
2014-08-20
![]() and
and
![]() corresponds to the even and odd traces of the data domain. At the start of the inverse transform,
corresponds to the even and odd traces of the data domain. At the start of the inverse transform,
![]() and
and
![]() will have just one trace of the coarsest scale of the seislet domain.
will have just one trace of the coarsest scale of the seislet domain.