 |
 |
 |
 | On anelliptic approximations for  velocities in
transversally isotropic media
velocities in
transversally isotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Shifted hyperbola approximation for
Up: On anelliptic approximations for
Previous: Exact expressions
Muir and Dellinger (1985) suggested representing anelliptic  phase
velocities with the following approximation:
phase
velocities with the following approximation:
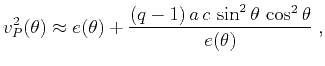 |
(12) |
where 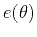 is the elliptical part of the velocity, defined by
is the elliptical part of the velocity, defined by
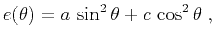 |
(13) |
and 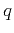 is the anellipticity coefficient (
is the anellipticity coefficient (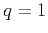 in case of elliptic
velocities). Approximation (12) uses only three parameters to
characterize the medium (
in case of elliptic
velocities). Approximation (12) uses only three parameters to
characterize the medium (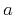 ,
, 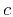 , and
, and 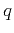 ) as opposed to the four parameters
(
) as opposed to the four parameters
(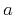 ,
, 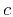 ,
, 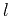 , and
, and 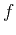 ) in the exact expression.
) in the exact expression.
There is some freedom in choosing an appropriate value for the coefficient
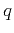 . Assuming near-vertical wave propagation and the vertical axis of symmetry
(a VTI medium) and fitting the curvature (
. Assuming near-vertical wave propagation and the vertical axis of symmetry
(a VTI medium) and fitting the curvature (
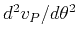 ) of the exact
phase velocity (4) near the vertical phase angle (
) of the exact
phase velocity (4) near the vertical phase angle (
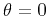 ),
leads to the definition (Dellinger et al., 1993)
),
leads to the definition (Dellinger et al., 1993)
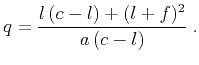 |
(14) |
In terms of Thomsen's elastic parameters 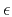 and
and 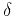 (Thomsen, 1986) and the elastic parameter
(Thomsen, 1986) and the elastic parameter 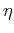 of
Alkhalifah and Tsvankin (1995),
of
Alkhalifah and Tsvankin (1995),
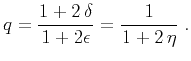 |
(15) |
This confirms the direct relationship between 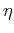 and anellipticity. If we
were to fit the phase velocity curvature near the horizontal axis
and anellipticity. If we
were to fit the phase velocity curvature near the horizontal axis
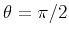 (perpendicular to the axis of symmetry), the appropriate value
for
(perpendicular to the axis of symmetry), the appropriate value
for 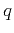 would be
would be
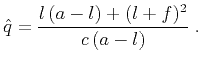 |
(16) |
Muir and Dellinger (1985) also suggested approximating the VTI
group velocity with an analogous expression
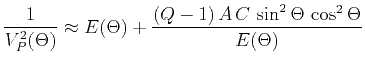 |
(17) |
where 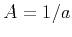 ,
, 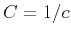 ,
, 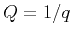 ,
, 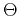 is the group angle, and
is the group angle, and
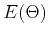 is the elliptical part:
is the elliptical part:
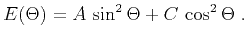 |
(18) |
Equations (12) and (17) are consistent in the sense
that both of them are exact for elliptic anisotropy (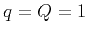 ) and
accurate to the first order in
) and
accurate to the first order in 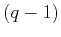 or
or 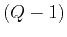 in the general case of
transversally isotropic media.
in the general case of
transversally isotropic media.
To the same approximation order, the connection between the phase and group
directions is
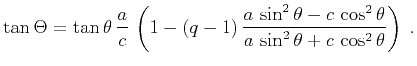 |
(19) |
 |
 |
 |
 | On anelliptic approximations for  velocities in
transversally isotropic media
velocities in
transversally isotropic media |  |
![[pdf]](icons/pdf.png) |
Next: Shifted hyperbola approximation for
Up: On anelliptic approximations for
Previous: Exact expressions
2014-05-14
![]() phase
velocities with the following approximation:
phase
velocities with the following approximation:
![]() . Assuming near-vertical wave propagation and the vertical axis of symmetry
(a VTI medium) and fitting the curvature (
. Assuming near-vertical wave propagation and the vertical axis of symmetry
(a VTI medium) and fitting the curvature (
![]() ) of the exact
phase velocity (4) near the vertical phase angle (
) of the exact
phase velocity (4) near the vertical phase angle (
![]() ),
leads to the definition (Dellinger et al., 1993)
),
leads to the definition (Dellinger et al., 1993)