 |
 |
 |
 | Seismic data interpolation using nonlinear shaping regularization |  |
![[pdf]](icons/pdf.png) |
Next: Field example
Up: Example
Previous: Example
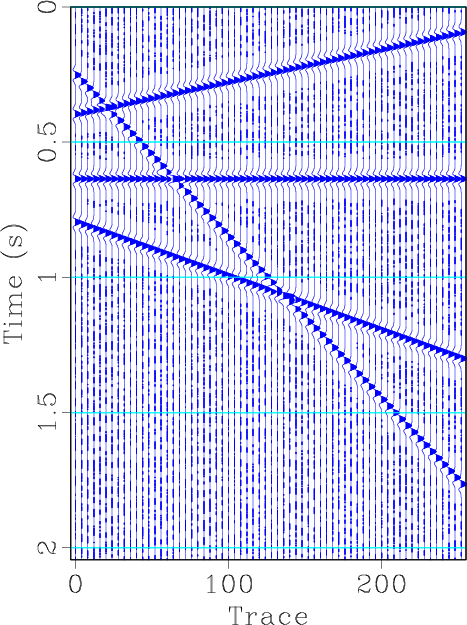
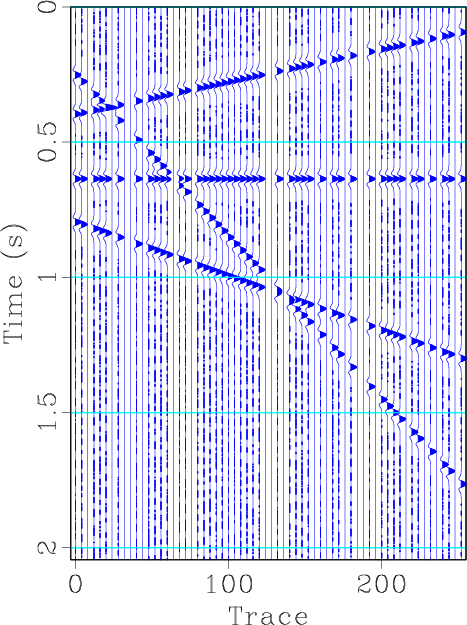
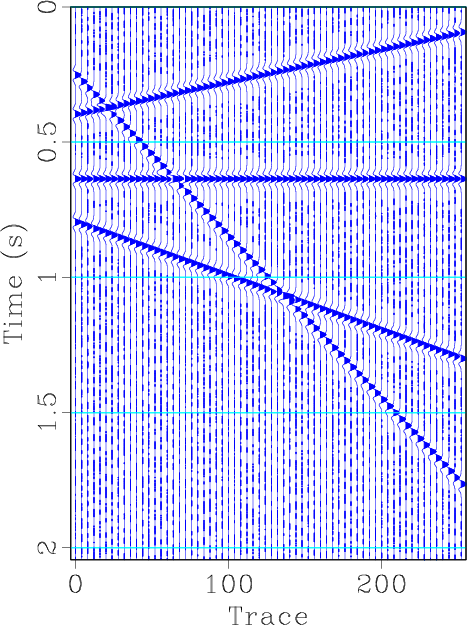
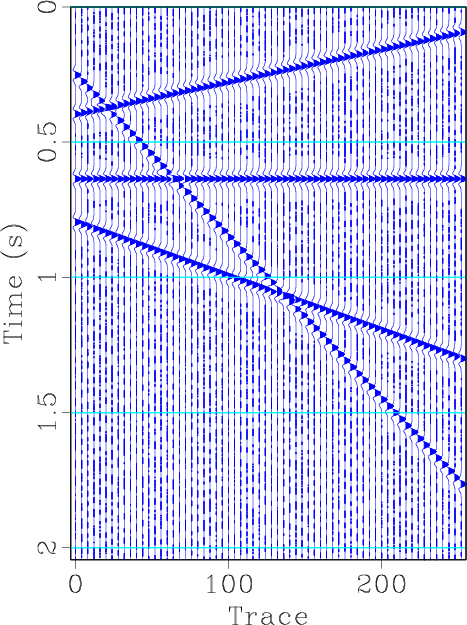
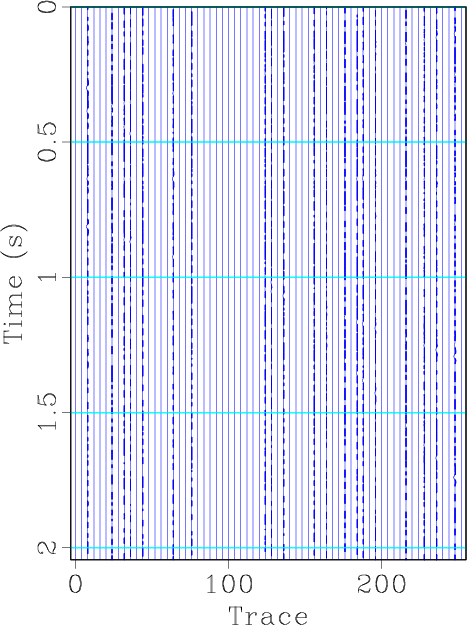
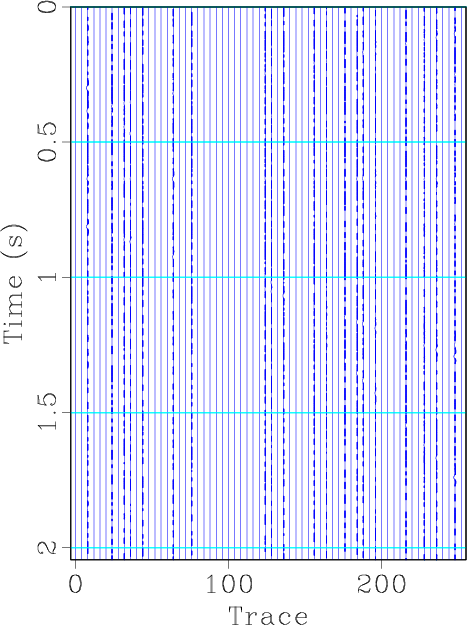
We first use a simple synthetic example (see Figure 1a) to demonstrate the interpolation effect of the faster version of shaping regularization. The synthetic data is composed of four different dipping events. We randomly removed 30% traces to form the irregularly sampled section (see Figure 1b). After applying the iterative interpolation formulation 6, and substituting
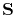 with
with
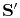 defined in equation 12 and 10, we get the interpolated section (see Figure 1d). The reconstructed result using the faster shaping regularization after only 20 iterations, as shown in Figure 1d, is nearly the same as the reconstructed result using the normal shaping regularization after 40 iterations, as shown in Figure 1c. This confirms that the normal and faster shaping regularizations can obtain the same converged results, but the faster shaping regularization can save the iteration cost greatly.The FK domain spectrum corresponding to each figure in Figure 1 are shown in Figure 2. Note that in this synthetic case
defined in equation 12 and 10, we get the interpolated section (see Figure 1d). The reconstructed result using the faster shaping regularization after only 20 iterations, as shown in Figure 1d, is nearly the same as the reconstructed result using the normal shaping regularization after 40 iterations, as shown in Figure 1c. This confirms that the normal and faster shaping regularizations can obtain the same converged results, but the faster shaping regularization can save the iteration cost greatly.The FK domain spectrum corresponding to each figure in Figure 1 are shown in Figure 2. Note that in this synthetic case
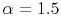 and
and
 .
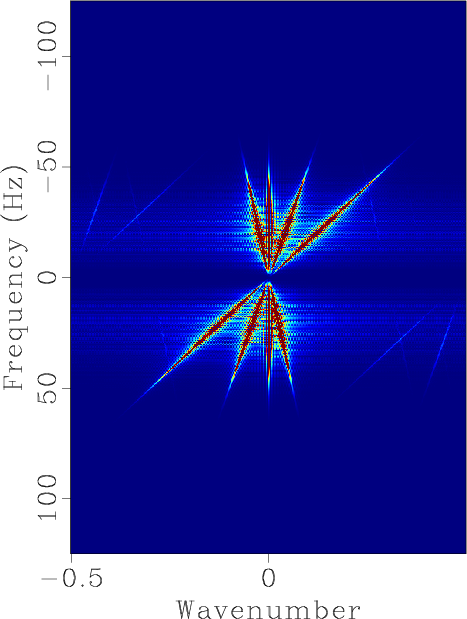
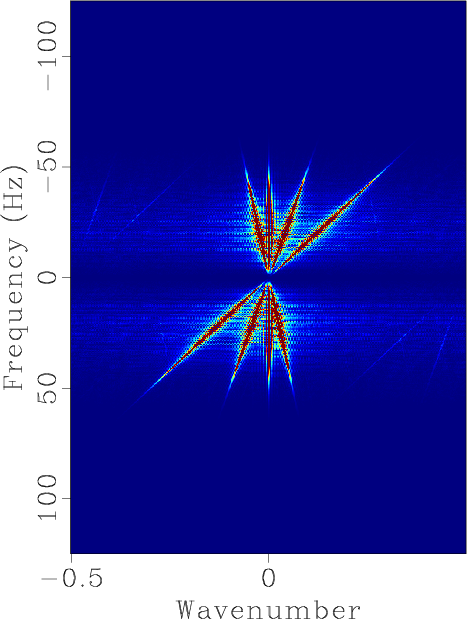
From Figures 1c and 1d , we find pleasant interpolation results because those missing traces are all filled up with coherent reflection components. Figure 2 further demonstrate the successful reconstruction, because the FK spectrum after interpolation is nearly the same as that of the original profile. Figure 3a shows the error section using shaping regularization after 40 iterations and Figure 3b shows the error section using faster shaping regularization after 20 iterations. The error sections shown in Figures 3a and 3b are nearly the same, which also confirms the faster convergence rate of the faster shaping regularization.
.
From Figures 1c and 1d , we find pleasant interpolation results because those missing traces are all filled up with coherent reflection components. Figure 2 further demonstrate the successful reconstruction, because the FK spectrum after interpolation is nearly the same as that of the original profile. Figure 3a shows the error section using shaping regularization after 40 iterations and Figure 3b shows the error section using faster shaping regularization after 20 iterations. The error sections shown in Figures 3a and 3b are nearly the same, which also confirms the faster convergence rate of the faster shaping regularization.
In order to test the convergence rate, we first define the measure to estimate the interpolation effect as
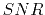 (Chen et al., 2015):
(Chen et al., 2015):
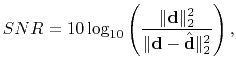 |
(15) |
where
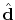 denotes the estimated model, and the unit of
denotes the estimated model, and the unit of 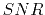 is
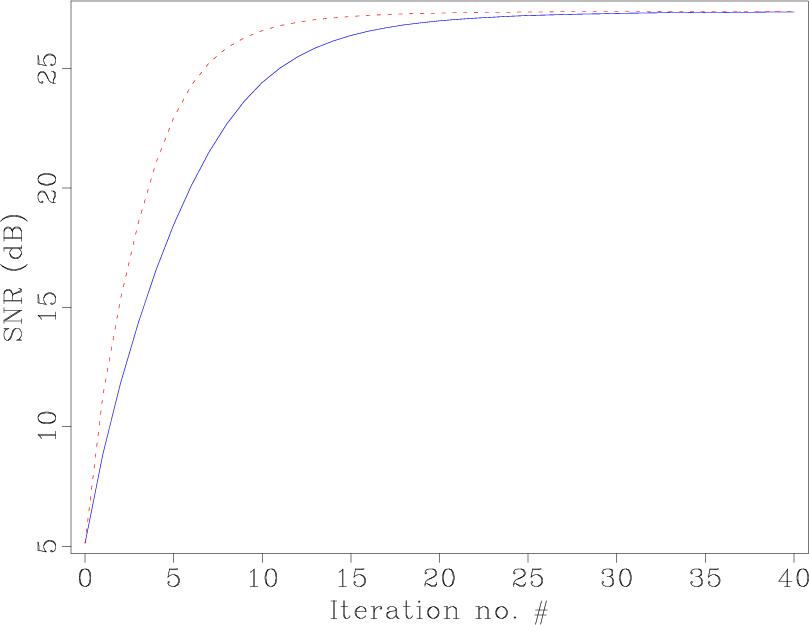
is 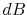 . Figure 4 shows the convergence diagrams of normal shaping regularization and faster shaping regularization. It's obvious that the proposed faster version can get a faster convergence.
. Figure 4 shows the convergence diagrams of normal shaping regularization and faster shaping regularization. It's obvious that the proposed faster version can get a faster convergence.
|
|---|
complex,complex-zero,complex-recon-o,complex-recon
Figure 1. Synthetic example demonstration for seismic interpolation using shaping regularization. (a) Original synthetic data. (b) Irregularly sampled section by randomly removing 30% traces. (c) Reconstructed section using shaping regularization after 40 iterations. (d) Reconstructed section using faster shaping regularization with 20 iterations.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|


|
|---|
complex-fk,complex-zerofk,complex-reconfk-o,complex-reconfk
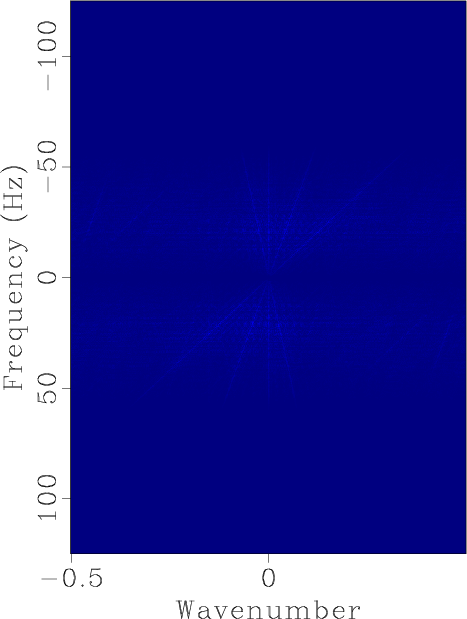
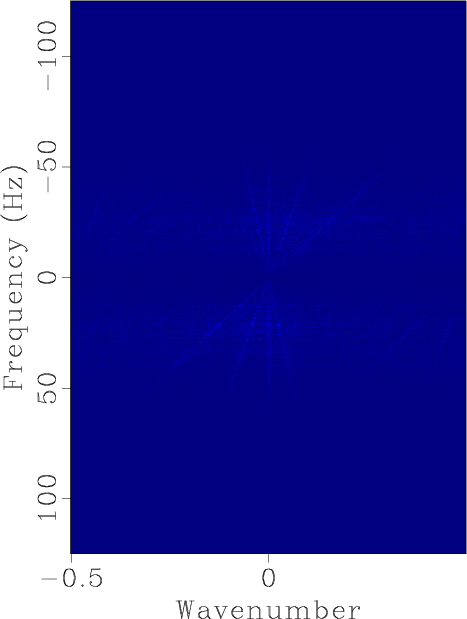
Figure 2. FK domain demonstration corresponding to Figure 1. (a) FK domain for original synthetic data. (b) FK domain for irregularly sampled section. (c) FK domain for reconstructed section using shaping regularization after 40 iterations. (d) FK domain for reconstructed section using faster shaping regularization after 20 iterations.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
|
|---|
complex-error-o,complex-error,complex-errorfk,complex-errorfk-o
Figure 3. Error sections demonstration for synthetic example. (a) Error section using shaping regularization after 40 iterations. (b) Error section using faster shaping regularization after 20 iterations. (c) FK domain of (a). (d) FK domain of (b).
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
|
|---|
SNRs
Figure 4. The SNR curves with normal and faster shaping regularization in the case of synthetic data. The solid line is for normal shaping regularization and the dashed line is for faster shaping regularization.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Seismic data interpolation using nonlinear shaping regularization |  |
![[pdf]](icons/pdf.png) |
Next: Field example
Up: Example
Previous: Example
2015-11-24
![]() (Chen et al., 2015):
(Chen et al., 2015):












