|
|
|
|
Adaptive multiple subtraction using regularized nonstationary regression |
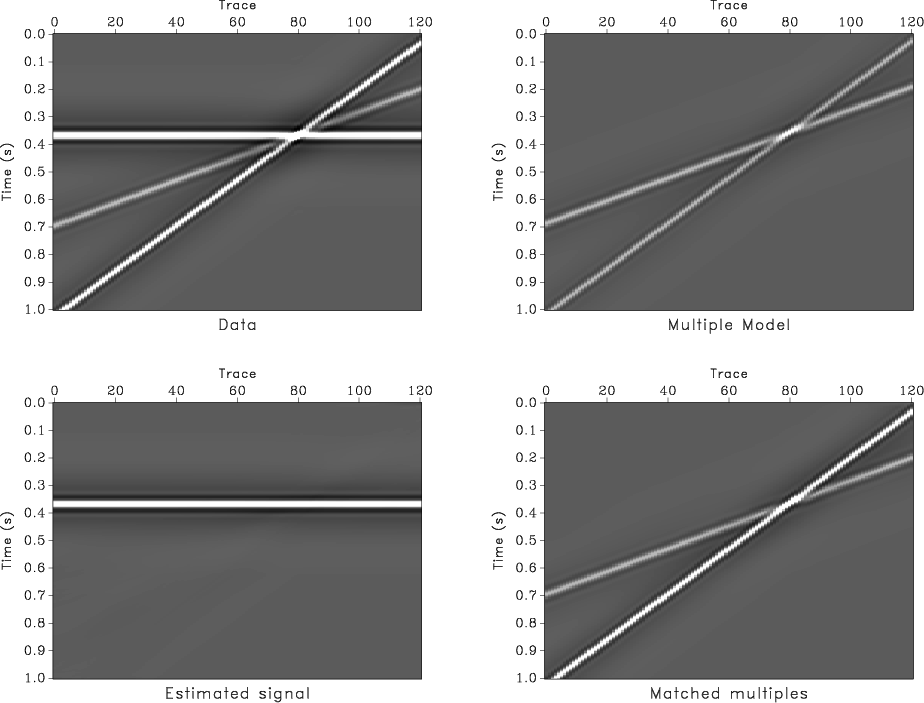
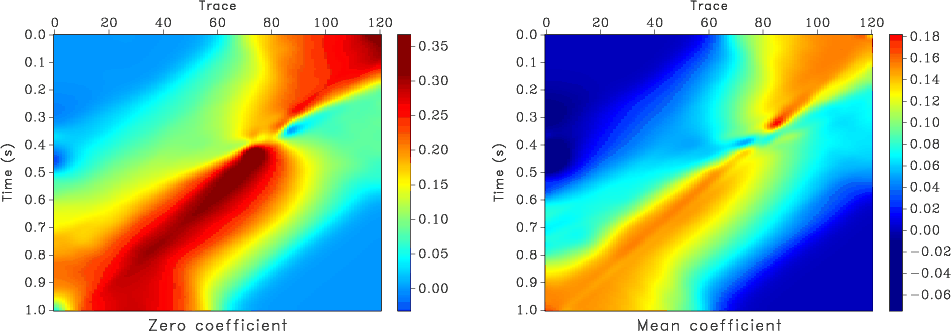
Abma et al. (2005) present a comparison of different adaptive subtraction algorithms used for multiple suppression. I use Abma's benchmark examples to illustrate an application of nonstationary regression to the adaptive subtraction problem. Figure 10 shows the first test: the input data (Figure 10a) contain a horizontal ``signal'' event and dipping ``noise'' events. We are provided with a model of the noise (Figure 10b). However, the model events are slightly shifted and have a different amplitude behavior. This test simulates a typical situation in adaptive surface-related multiple elimination, where there are phase and amplitude distortions in the multiple model, caused by an imperfect prediction. To handle the variability in noise amplitudes, I design a non-stationary matching filter with 13 coefficients and 3-sample smoothing radius and apply it to match the noise model to the data. Subtracting matched noise (Figure 10d) produces the desired and nearly perfect signal estimate (Figure 10c). The variability of filter coefficients is illustrated in Figure 11, which displays the zero-lag coefficient and the mean coefficient of the non-stationary matching filter.
|
|---|
|
planes
Figure 10. Benchmark test on adaptive subtraction from Abma et al. (2005). a - Input synthetic data. b - Model of the noise containing amplitude and phase differences with respect to the corresponding part of the data. c - Extracted signal. d - Estimated noise. |
|
|
|
|---|
|
filt
Figure 11. Variability of non-stationary match filter coefficients for the example shown in Figure 10. a - Zero-lag coefficient. b - Mean coefficient. |
|
|
|
|---|
|
curves
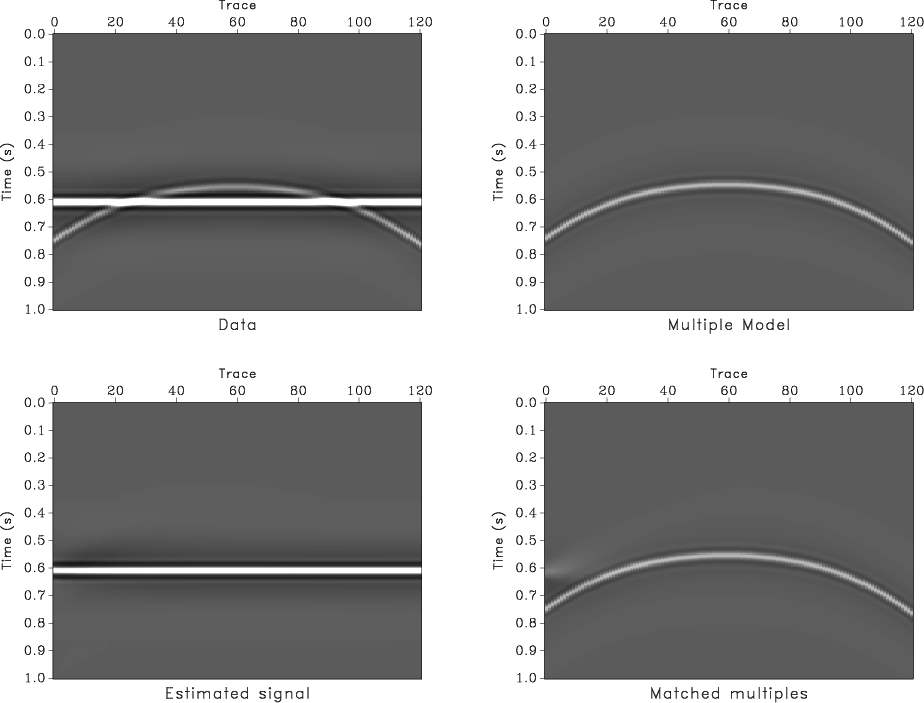
Figure 12. Benchmark test on adaptive subtraction from Abma et al. (2005). a - Input synthetic data. b - Model of the noise containing amplitude and phase differences with respect to the corresponding part of the data. c - Extracted signal. d - Estimated noise. |
|
|
|
|---|
|
dfilt
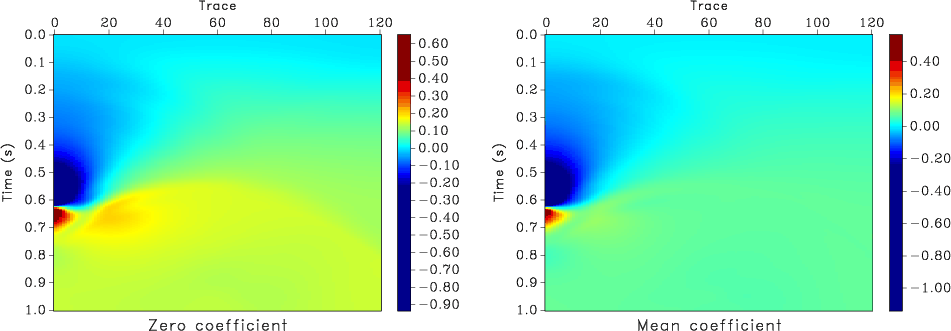
Figure 13. Variability of non-stationary match filter coefficients for the example shown in Figure 12. a - Zero-lag coefficient. b - Mean coefficient. |
|
|
Another benchmark from Abma et al. (2005) is shown in Figure 12. This time, the noise part of the data is a curved event which has a predictive model (Figure 12b) with some amplitude and phase differences. Non-stationary regularized regression correctly predicts the noise signal (Figure 12d) using match filtering and produces an accurate signal estimate (Figure 12c). The variability of non-stationary filter coefficients is shown in Figure 13.
|
|
|
|
Adaptive multiple subtraction using regularized nonstationary regression |