|
|
|
|
OC-seislet: seislet transform construction with differential offset continuation |
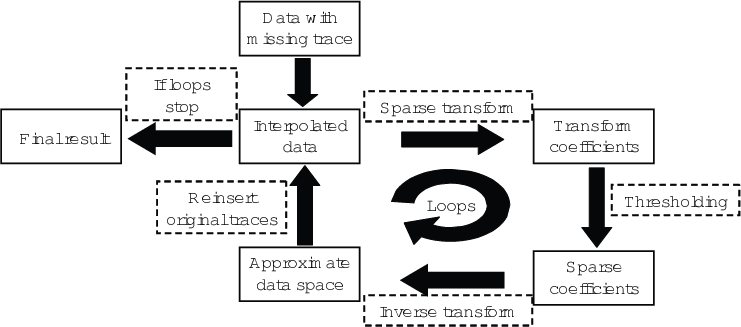
The proposed OC-seislet transform uses physical offset continuation to compress the reflection data after NMO and log-stretch transform of the time coordinate, followed by double Fourier transforms of the stretched time axis and midpoint axis. If seismic traces in the midpoint direction are missing, the Fourier transform may produce artifacts (spatial leakage) along the midpoint-wavenumber axis (Zwartjes and Gisolf, 2007). Additionally, the missing seismic traces in the offset direction affect the continuity of predicted data. Once the OC-seislet transform is applied for predicting and compressing, the artifacts, discontinuity information, and random noise spread over different scales while the predictable reflection information gets compressed to large coefficients at small scales. A simple thresholding method can easily remove the small coefficients of artifacts. Finally, applying inverse OC-seislet transform, inverse FFTs both in time and midpoint axes, inverse log-stretch, and inverse NMO reconstructs the data while attenuating random noise, reducing artifacts along the midpoint axis, reconstructing continuity in the offset axis, and recovering main structural features without using any assumptions about structural continuity in the midpoint-offset-time domain. The key steps are shown in Figure 5a.
The idea of sparse transforms has been thoroughly explored in the literature, with application to Fourier and curvelet transforms. Liu and Sacchi (2004) proposed a Fourier-based minimum weighted norm interpolation (MWNI) algorithm with iterative inversion to perform multidimensional reconstruction of seismic wavefields. Xu et al. (2005) suggested an iterative Fourier-based matching pursuit (antileakage Fourier transform) for seismic data regularization. Abma and Kabir (2006) used a Fourier-based method with iterative thresholding to solve seismic data interpolation problems. Herrmann and Hennenfent (2008) presented a recovery method that exploits the curvelet frame. Missing data interpolation is a particular case of data regularization, where the input data are already given on a regular grid, and one needs to reconstruct only the missing values in empty bins (Fomel, 2001). For input data with nonuniform spatial sampling, one can bin the data to a regular grid first and then use the proposed method for filling empty bins. It is also possible to generalize the method for combining irregular data interpolation with a sparse transform (Zwartjes and Gisolf, 2007). The thresholding iteration helps a sparse transform to recover the missing information. We adopt a similar thresholding strategy (fixed thresholding value for each iteration) with the OC-seislet transform. The key steps of the algorithm are illustrated schematically in Figure 5b.

|
|---|
|
denoise,jpocs
Figure 5. Schematic illustration of the thresholding workflow. Denoising with a simple soft-thresholding (a) and missing data interpolation with iterative soft-thresholding (b). |
|
|
|
|
|
|
OC-seislet: seislet transform construction with differential offset continuation |