|
|
|
|
Omnidirectional plane-wave destruction |
Dip estimation by OPWD is equivalent to the parameter estimation
of the OPWD filter in equation 17.
The desired parameters ![]() minimize the predictive error:
minimize the predictive error:
| (18) |
| (19) |
We solve the above equation set by Newton's search.
At each iteration,
the increments
![]() are calculated
from the following linearization:
are calculated
from the following linearization:
![$\displaystyle \left[ \begin{array}{cc} \displaystyle{\frac{\partial H_4}{\parti...
... \approx \left[ \begin{array}{c} -H_4U r^2-p_1^2-p_2^2 \end{array}\right]\;.$](img98.png) |
(20) |
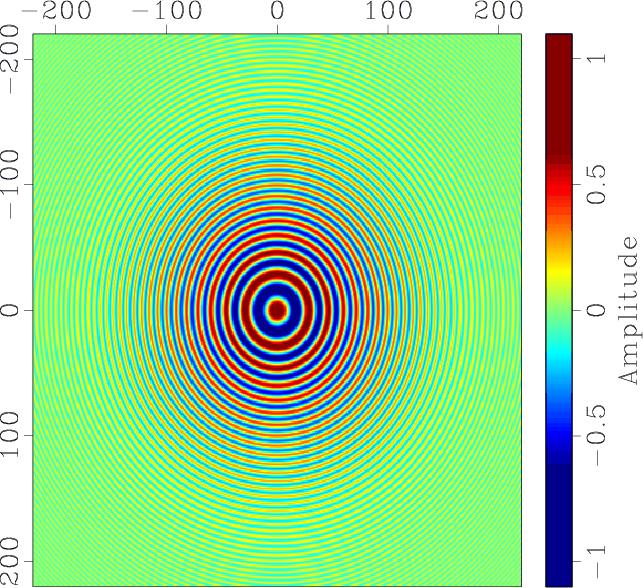
In order to test the performance of OPWD, we generate a 2D synthetic image in polar coordinates using the following equation:
Structures in this image have constant dip angles along radial directions,
but the frequency and magnitude vary with radius.
Figure 6a shows a test example
with
![]() .
We apply the
first-order (
.
We apply the
first-order (![]() ) OPWD filter to this test image.
With the starting dip
) OPWD filter to this test image.
With the starting dip
![]() ,
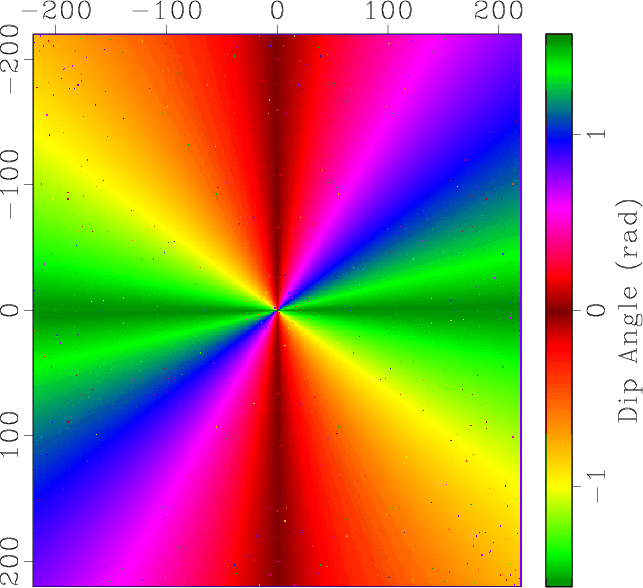
we obtain an estimation result in 10 iterations,
as shown in Figure 6b.
Obviously, dip estimation by OPWD is effective
for both horizontal and vertical structures.
,
we obtain an estimation result in 10 iterations,
as shown in Figure 6b.
Obviously, dip estimation by OPWD is effective
for both horizontal and vertical structures.
|
|---|
|
circle,odip,oerr,lerr
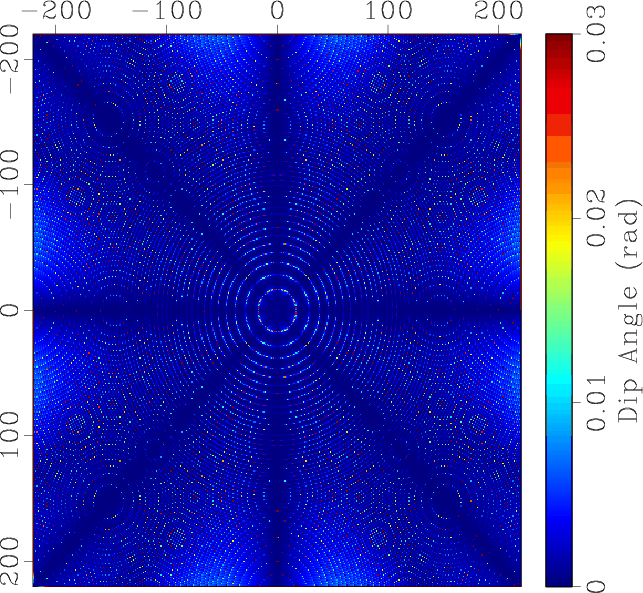
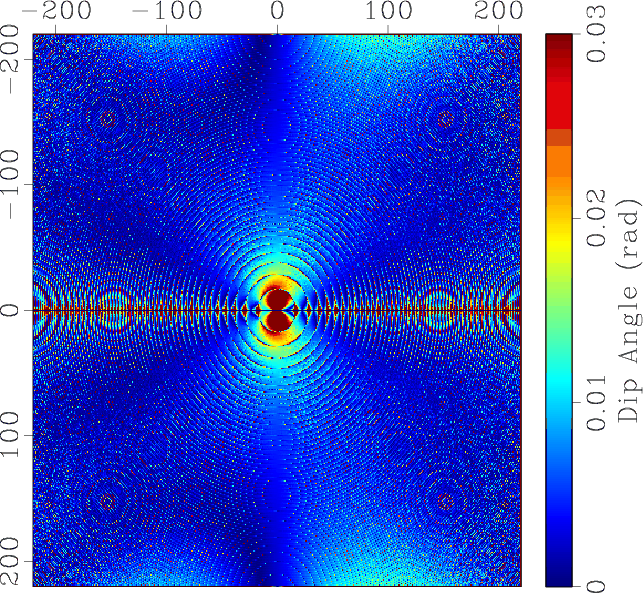
Figure 6. An omnidirectional dip estimation example: (a) test image; (b) dip angles estimated by the OPWD filter; (c) estimation error of OPWD; (d) estimation error of LPWD. |
|
|
We compare the proposed OPWD with LPWD by estimating errors in Figures 6c and 6d. As the test image is noise-free, we do not need to use any smoothing regularization in both of these methods. In this case, the modeling errors are the dominate factor of the final estimating errors. Obviously, the LPWD cannot detect the vertical structure accurately, while the OPWD can.
|
|
|
|
Omnidirectional plane-wave destruction |