 |
 |
 |
 | A fast algorithm for 3D azimuthally anisotropic velocity scan |  |
![[pdf]](icons/pdf.png) |
Next: Fast 3D butterfly algorithm
Up: Theory
Previous: Theory
The right-hand side of equation 5 is a quotient of two (discrete) generalized Radon transforms (Beylkin, 1984). They can be expressed in a unified way as (to simplify the notation, we write
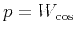 ,
,
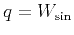 in this and next subsections)
in this and next subsections)
 |
(7) |
where 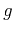 is
is 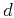 or some composite function of
or some composite function of 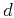 .
.
To construct the fast algorithm, we first rewrite equation 7 in the frequency domain as
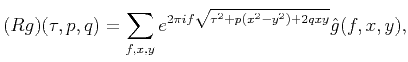 |
(8) |
where  is frequency and
is frequency and
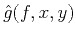 is the Fourier transform of
is the Fourier transform of 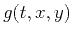 in time. We next perform a linear transformation to map all discrete points in
in time. We next perform a linear transformation to map all discrete points in 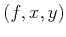 and
and
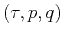 domains to points in the unit cube
domains to points in the unit cube ![$ [0,1]^3$](img53.png) ; i.e., a point
; i.e., a point
 min
min max
max![$ ]\times[x_$](img56.png) min
min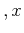 max
max![$ ]\times [y_$](img58.png) min
min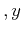 max
max![$ ]$](img60.png) is mapped to
is mapped to
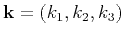
![$ \in[0,1]\times[0,1]\times[0,1]=K$](img62.png) via
via
| |
|
 max max min min min min |
|
| |
|
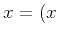 max max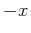 min min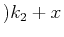 min min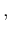 |
|
| |
|
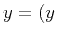 max max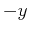 min min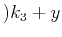 min min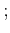 |
|
a point
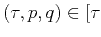 min
min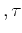 max
max![$ ]\times[p_$](img76.png) min
min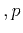 max
max![$ ]\times[q_$](img78.png) min
min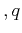 max
max![$ ]$](img60.png) is mapped to
is mapped to
![$ \mathbf{x}=(x_1,x_2,x_3)\in[0,1]\times[0,1]\times[0,1]=X$](img80.png) via
via
| |
|
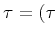 max max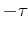 min min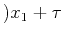 min min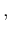 |
|
| |
|
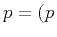 max max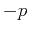 min min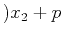 min min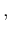 |
|
| |
|
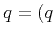 max max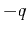 min min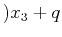 min min |
|
If we define a phase function
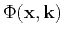 as
as
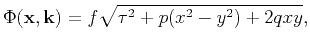 |
(9) |
then equation 8 can be recast as
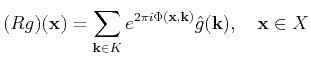 |
(10) |
(throughout the paper, 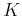 and
and 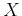 are used to denote either sets of discrete points or the cubic
domains containing them).
are used to denote either sets of discrete points or the cubic
domains containing them).
 |
 |
 |
 | A fast algorithm for 3D azimuthally anisotropic velocity scan |  |
![[pdf]](icons/pdf.png) |
Next: Fast 3D butterfly algorithm
Up: Theory
Previous: Theory
2015-03-27
![]() ,
,
![]() in this and next subsections)
in this and next subsections)