 |
 |
 |
 | Shaping regularization in geophysical estimation problems |  |
![[pdf]](icons/pdf.png) |
Next: Shaping regularization in theory
Up: Fomel: Shaping regularization
Previous: Review of Tikhonov's regularization
Let us consider an application of Tikhonov's regularization to one of the simplest
possible estimation problems: smoothing. The task of smoothing is to find a
model 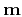 that fits the observed data
that fits the observed data 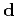 but is in a
certain sense smoother. In this case, the forward operator
but is in a
certain sense smoother. In this case, the forward operator 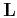 is
simply the identity operator, and the formal solutions 1 and 3 take the form
is
simply the identity operator, and the formal solutions 1 and 3 take the form
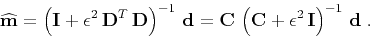 |
(5) |
Smoothness is controlled by the choice of the regularization
operator 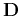 and the scaling parameter
and the scaling parameter 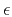 .
.
Figure 1 shows the impulse response of the regularized
smoothing operator in the 1-D case when 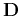 is the first difference operator. The impulse response has exponentially
decaying tails. Repeated application of smoothing in this case is
equivalent to applying an implicit Euler finite-difference scheme to
the solution of the diffusion equation
is the first difference operator. The impulse response has exponentially
decaying tails. Repeated application of smoothing in this case is
equivalent to applying an implicit Euler finite-difference scheme to
the solution of the diffusion equation
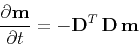 |
(6) |
The impulse response converges to a Gaussian bell-shape curve in the physical
domain, while its spectrum converges to a Gaussian in the frequency domain.

|
|---|
exp
Figure 1. Left: impulse response of regularized
smoothing. Repeated smoothing converges to a Gaussian bell shape. Right:
frequency spectrum of regularized smoothing. The spectrum also converges to
a Gaussian.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
As far as the smoothing problem is concerned, there are better ways to
smooth signals than applying
equation 5. One example is triangle
smoothing (Claerbout, 1992). To define triangle
smoothing of one-dimensional signals, start with box smoothing, which,
in the 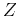 -transform notation, is a convolution with the filter
-transform notation, is a convolution with the filter
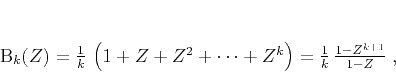 |
(7) |
where  is the filter length. Form a triangle smoother by
correlation of two boxes
is the filter length. Form a triangle smoother by
correlation of two boxes
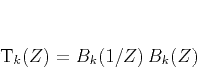 |
(8) |
Triangle smoothing is more
efficient than regularized smoothing, because it requires twice less
floating point multiplications. It also provides smoother results
while having a compactly supported impulse response
(Figure 2). Repeated application of triangle smoothing
also makes the impulse response converge to a Gaussian shape but at a
significantly faster rate.
One can also implement smoothing by Gaussian filtering in the frequency domain
or by applying other types of bandpass filters.
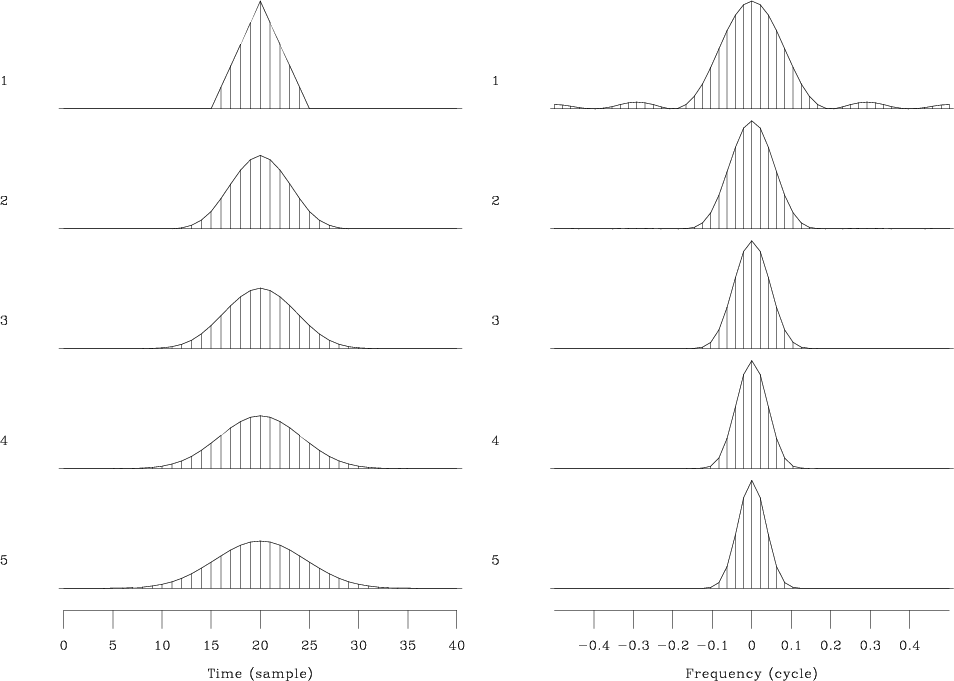
|
|---|
tri
Figure 2. Left: impulse response of triangle
smoothing. Repeated smoothing converges to a Gaussian bell shape. Right:
frequency spectrum of triangle smoothing. Convergence to
a Gaussian is faster than in the case of regularized smoothing. Compare to
Figure 1.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Shaping regularization in geophysical estimation problems |  |
![[pdf]](icons/pdf.png) |
Next: Shaping regularization in theory
Up: Fomel: Shaping regularization
Previous: Review of Tikhonov's regularization
2013-07-26
![]() is the first difference operator. The impulse response has exponentially
decaying tails. Repeated application of smoothing in this case is
equivalent to applying an implicit Euler finite-difference scheme to
the solution of the diffusion equation
is the first difference operator. The impulse response has exponentially
decaying tails. Repeated application of smoothing in this case is
equivalent to applying an implicit Euler finite-difference scheme to
the solution of the diffusion equation

![]() -transform notation, is a convolution with the filter
-transform notation, is a convolution with the filter
