 |
 |
 |
 | Shaping regularization in geophysical estimation problems |  |
![[pdf]](icons/pdf.png) |
Next: From triangle smoothing to
Up: Fomel: Shaping regularization
Previous: Smoothing by regularization
The idea of shaping regularization starts with recognizing smoothing
as a fundamental operation. In a more general sense, smoothing implies
mapping of the input model to the space of admissible functions. I
call the mapping operator shaping. Shaping operators do not
necessarily smooth the input but they translate it into an acceptable
model.
Taking equation 5 and using it as the
definition of the regularization operator 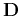 , we can write
, we can write
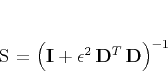 |
(9) |
or
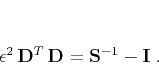 |
(10) |
Substituting equation 10
into 1 yields a formal solution of the
estimation problem regularized by shaping:
![\begin{displaymath}
\widehat{\mathbf{m}} =
\left(\mathbf{L}^T\,\mathbf{L} + \...
...ight)\right]^{-1}\,
\mathbf{S}\,\mathbf{L}^T\,\mathbf{d}\;.
\end{displaymath}](img33.png) |
(11) |
The meaning of equation 11 is easy to
interpret in some special cases:
- If
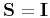 (no shaping applied), we obtain the solution of
unregularized problem.
(no shaping applied), we obtain the solution of
unregularized problem.
- If
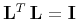 (
(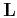 is a unitary operator),
the solution is simply
is a unitary operator),
the solution is simply
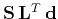 and does not require
any inversion.
and does not require
any inversion.
- If
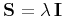 (shaping by scaling), the
solution approaches
(shaping by scaling), the
solution approaches
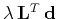 as
as 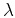 goes to
zero.
goes to
zero.
The operator 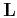 may have physical units that require
scaling. Introducing scaling of
may have physical units that require
scaling. Introducing scaling of 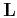 by
by 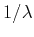 in
equation 11, we can rewrite it as
in
equation 11, we can rewrite it as
![\begin{displaymath}
\widehat{\mathbf{m}} =
\left[\lambda^2\,\mathbf{I} +
\m...
...ht)
\right]^{-1}\,
\mathbf{S}\,\mathbf{L}^T\,\mathbf{d}\;.
\end{displaymath}](img41.png) |
(12) |
The 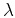 scaling in equation 12
controls the relative scaling of the forward operator
scaling in equation 12
controls the relative scaling of the forward operator 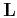 but
not the shape of the estimated model, which is controlled by the
shaping operator
but
not the shape of the estimated model, which is controlled by the
shaping operator 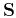 .
.
Iterative inversion with the conjugate-gradient algorithm requires
symmetric positive definite operators (Hestenes and Steifel, 1952). The inverse
operator in equation 12 can be symmetrized when the
shaping operator is symmetric and representable in the form
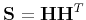 with a square and invertible
with a square and invertible  . The
symmetric form of equation 12 is
. The
symmetric form of equation 12 is
![\begin{displaymath}
\widehat{\mathbf{m}} =
\mathbf{H}\,\left[\lambda^2\,\math...
...}\right]^{-1}\,
\mathbf{H}^T\,\mathbf{L}^T\,\,\mathbf{d}\;.
\end{displaymath}](img44.png) |
(13) |
When the inverted matrix
is positive definite, equation 13 is suitable for an
iterative inversion with the conjugate-gradient algorithm. Appendix A
contains a complete algorithm description.
 |
 |
 |
 | Shaping regularization in geophysical estimation problems |  |
![[pdf]](icons/pdf.png) |
Next: From triangle smoothing to
Up: Fomel: Shaping regularization
Previous: Smoothing by regularization
2013-07-26
![]() , we can write
, we can write
![]() may have physical units that require
scaling. Introducing scaling of
may have physical units that require
scaling. Introducing scaling of ![]() by
by ![]() in
equation 11, we can rewrite it as
in
equation 11, we can rewrite it as
![]() with a square and invertible
with a square and invertible ![]() . The
symmetric form of equation 12 is
. The
symmetric form of equation 12 is