 |
 |
 |
 | Nonlinear structure-enhancing filtering using plane-wave prediction |  |
![[pdf]](icons/pdf.png) |
Next: Appendex B: Lower-upper-middle filter
Up: Liu etc.: Structurally nonlinear
Previous: Acknowledgments
Fomel (2007a) defined local similarity as follows. The global
correlation coefficient between two different signals 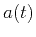 and
and
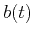 is the functional
is the functional
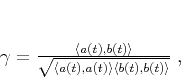 |
(5) |
where
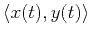 denotes the dot product between two signals
denotes the dot product between two signals
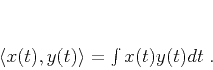 |
(6) |
In a linear algebra notation, the squared correlation coefficient  from equation A-1 can be represented as a product of two
least-squares inverses
from equation A-1 can be represented as a product of two
least-squares inverses
 |
(7) |
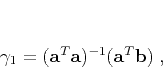 |
(8) |
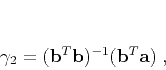 |
(9) |
where 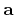 is a vector notation for
is a vector notation for 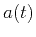 ,
, 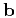 is a
vector notation for
is a
vector notation for 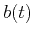 , and
, and
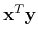 denotes the
dot product operation defined in equation A-2. Let
denotes the
dot product operation defined in equation A-2. Let
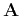 be a diagonal operator composed of the elements of
be a diagonal operator composed of the elements of
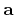 and
and 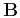 be a diagonal operator composed of the
elements of
be a diagonal operator composed of the
elements of 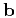 . Localizing equations A-4
and A-5 amounts to adding regularization to
inversion. Scalars
. Localizing equations A-4
and A-5 amounts to adding regularization to
inversion. Scalars 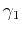 and
and 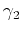 turn into vectors
turn into vectors
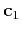 and
and 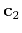 defined, using shaping
regularization (Fomel, 2007b)
defined, using shaping
regularization (Fomel, 2007b)
![\begin{displaymath}
\mathbf{c}_1 = [\lambda^2 \mathbf{I} + \mathbf{S}(\mathbf...
...\lambda^2 \mathbf{I})]^{-1}\mathbf{S}\mathbf{A}^T\mathbf{b}\;,
\end{displaymath}](img49.png) |
(10) |
![\begin{displaymath}
\mathbf{c}_2 = [\lambda^2 \mathbf{I} + \mathbf{S}(\mathbf...
...\lambda^2 \mathbf{I})]^{-1}\mathbf{S}\mathbf{B}^T\mathbf{a}\;,
\end{displaymath}](img50.png) |
(11) |
where 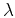 scaling controls the relative scaling of operators
scaling controls the relative scaling of operators
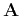 and
and 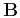 . Finally, the componentwise product of
vectors
. Finally, the componentwise product of
vectors 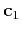 and
and 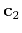 defines the local similarity
measure.
defines the local similarity
measure.
For using time-dependent smooth weights in the stacking process, the
local similarity amplitude can be chosen as a weight for stacking
seismic data. We thus stack only those parts of the predicted data whose
similarity to the reference one is comparatively large (Liu et al., 2009a).
 |
 |
 |
 | Nonlinear structure-enhancing filtering using plane-wave prediction |  |
![[pdf]](icons/pdf.png) |
Next: Appendex B: Lower-upper-middle filter
Up: Liu etc.: Structurally nonlinear
Previous: Acknowledgments
2013-07-26
![]() and
and
![]() is the functional
is the functional
![]() from equation A-1 can be represented as a product of two
least-squares inverses
from equation A-1 can be represented as a product of two
least-squares inverses