|
|
|
|
Simulating propagation of decoupled elastic waves using low-rank approximate mixed-domain integral operators for anisotropic media |
|
|---|
|
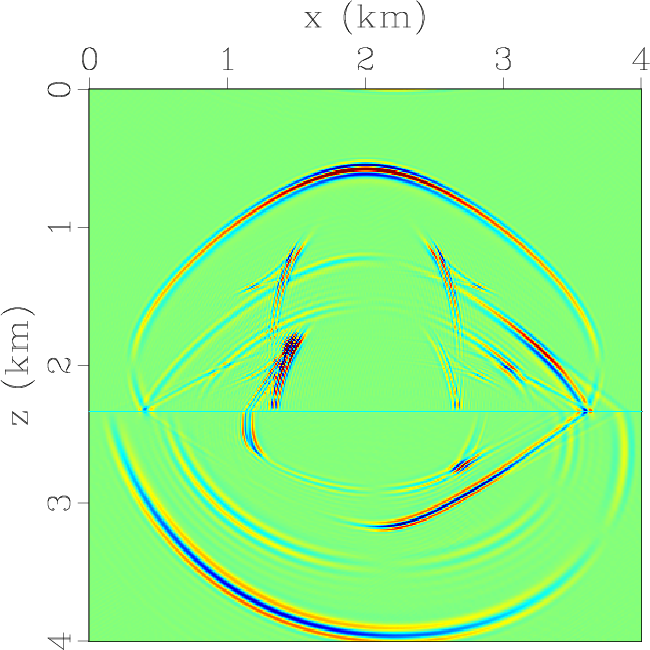
ElasticxKSSInterf,ElasticzKSSInterf
Figure 1. Horizontal and vertical components of the elastic wavefields at the time of 0.3 s synthesized by solving the 2nd-order elastic wave equation with |
|
|
|
|---|
|
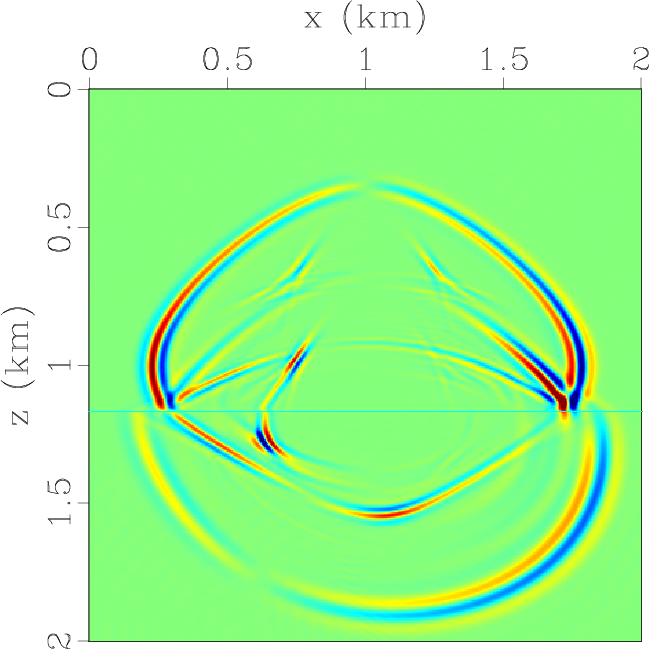
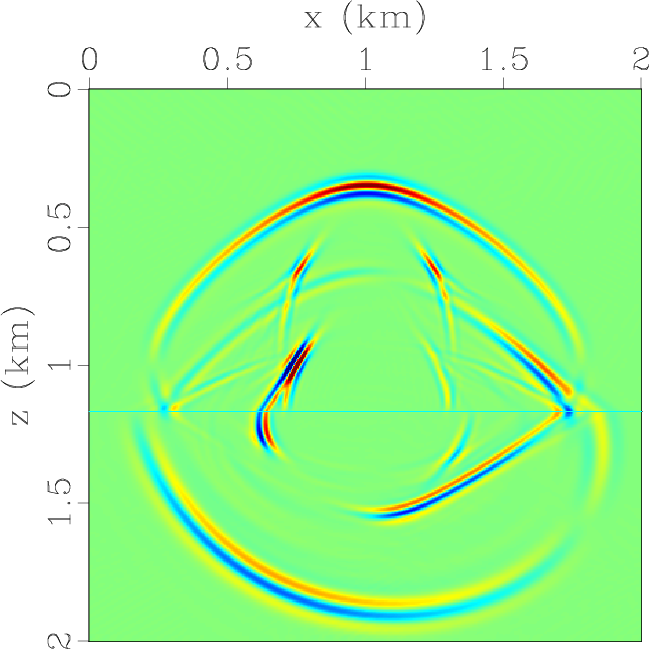
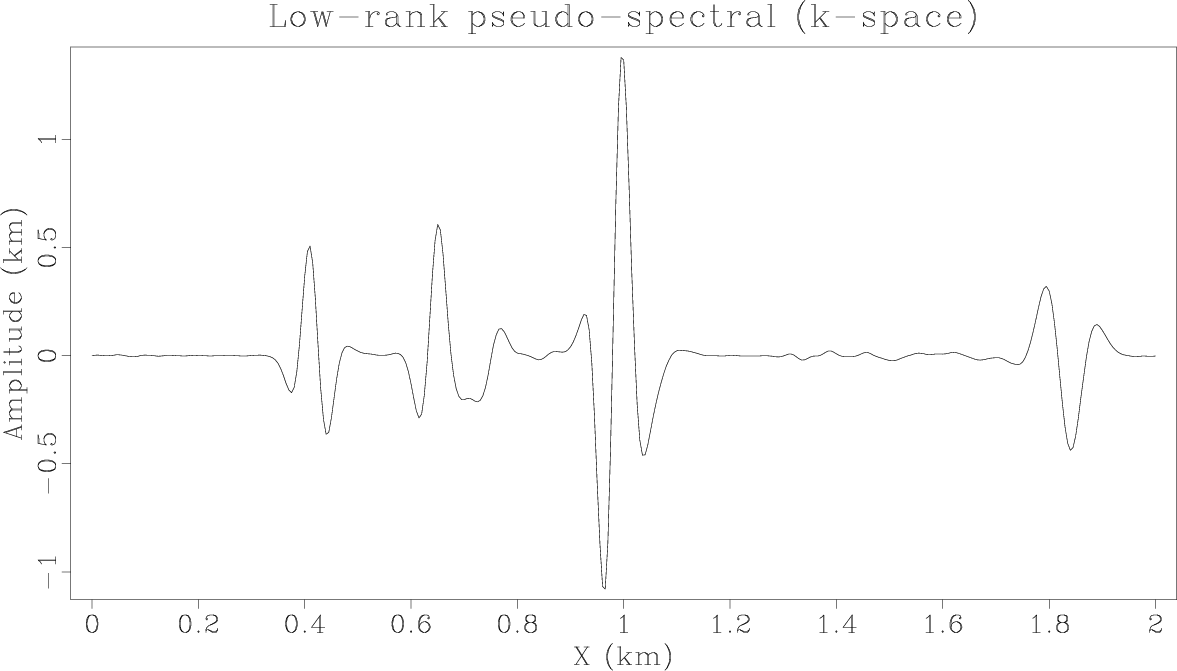
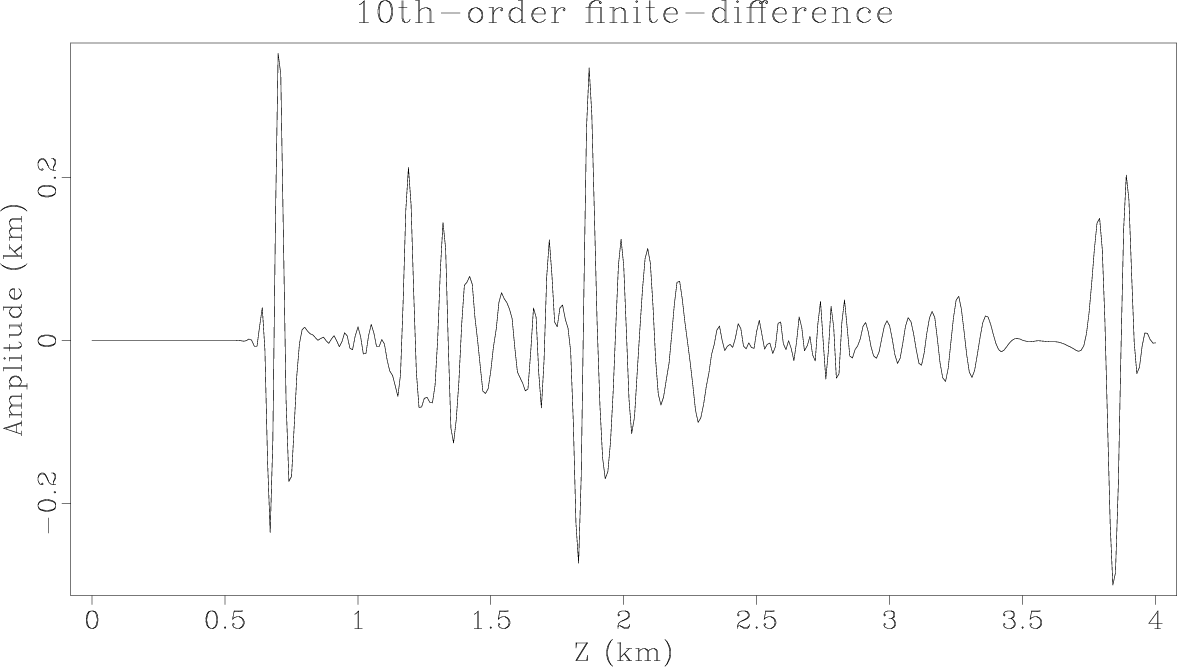
ElasticzFDwave,ElasticzPSLRwave,ElasticzKSwave
Figure 2. Vertical slices through the vertical components of the synthetic elastic wavefields at |
|
|


|
|---|
|
ElasticzFDInterfC,ElasticzPSLRInterfC,ElasticzKSSInterfC
Figure 3. Vertical components of the elastic wavefields at the time of 0.6 s synthesized using three schemes with the same spatial sampling |
|
|
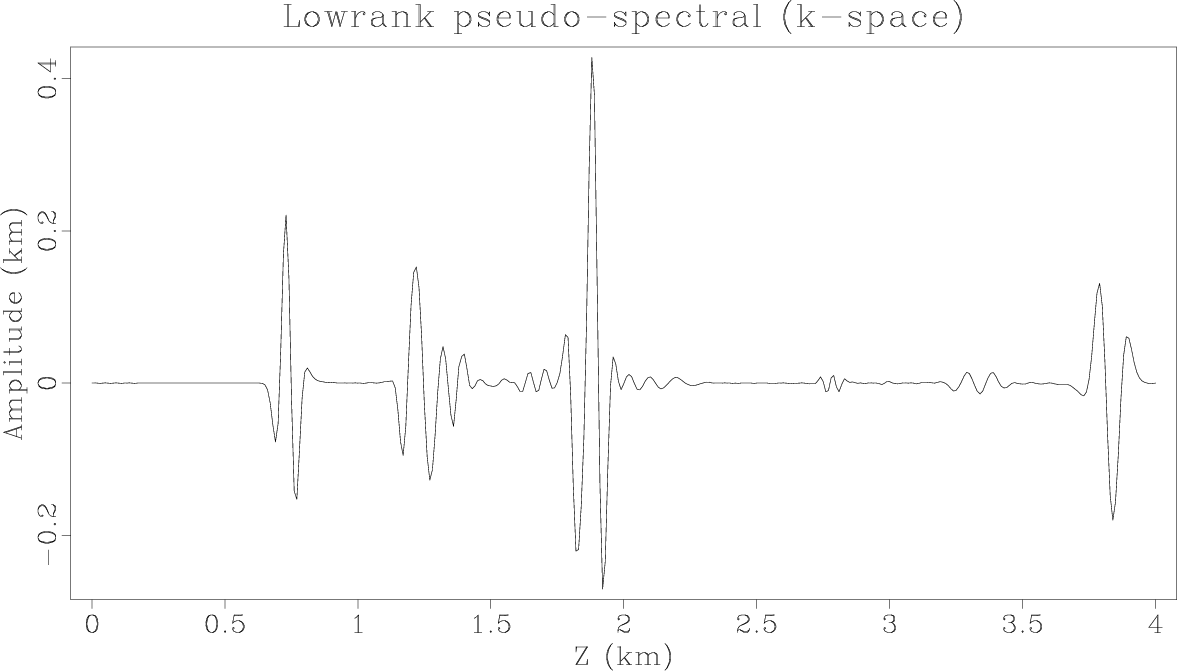
|
|---|
|
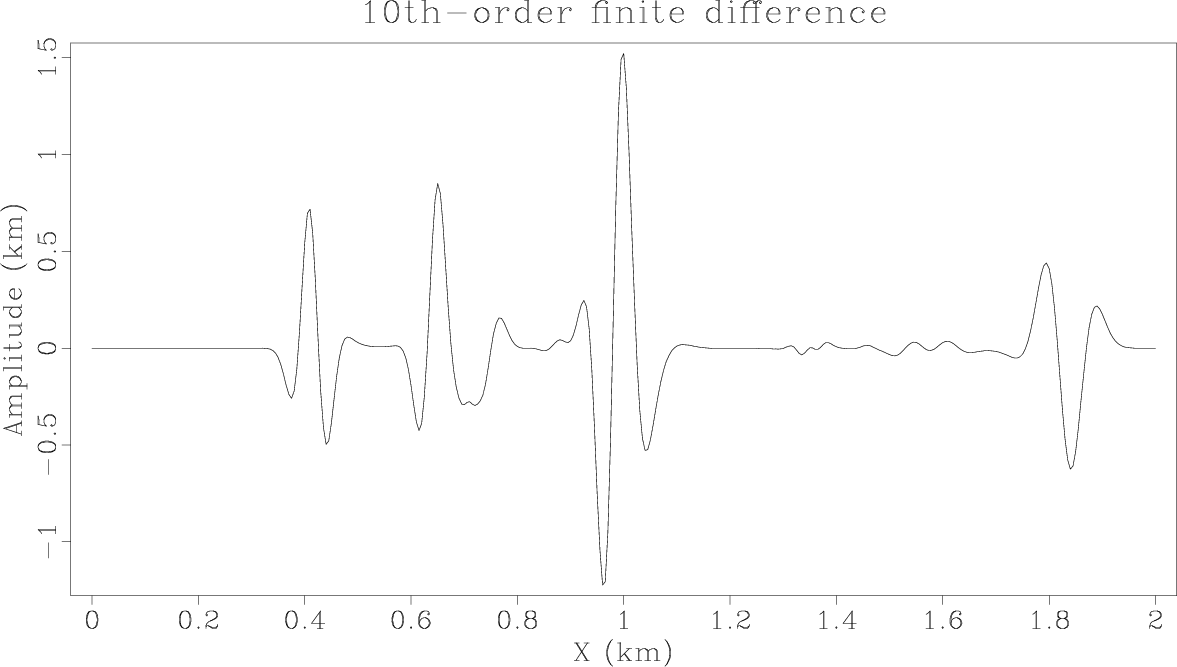
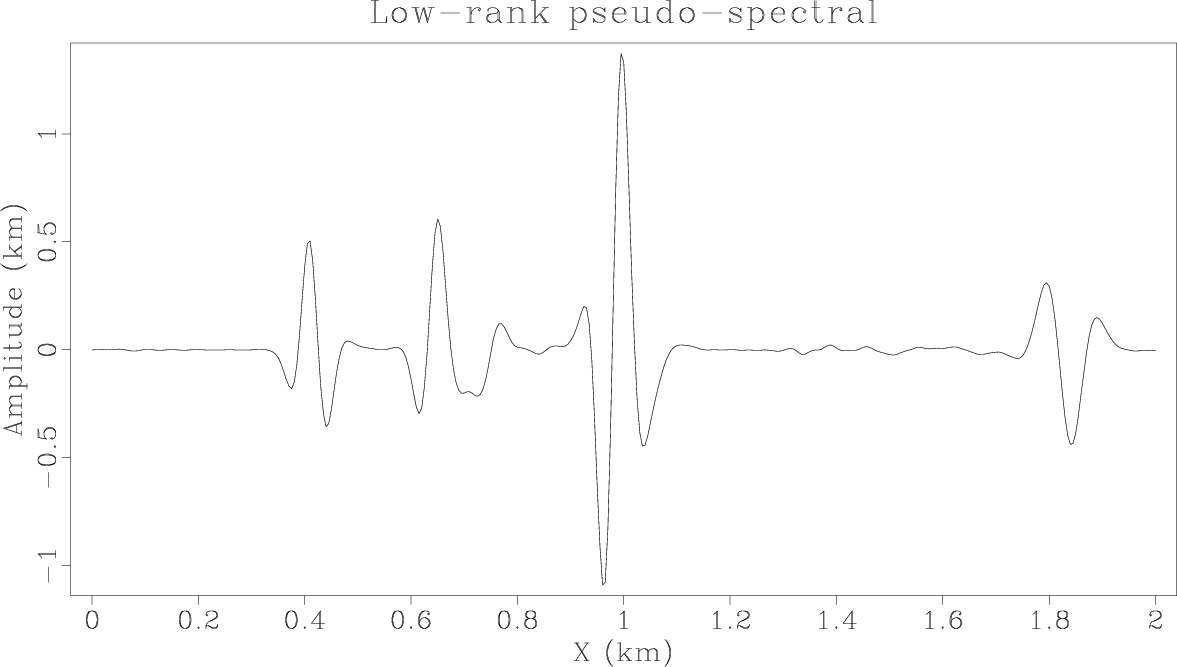
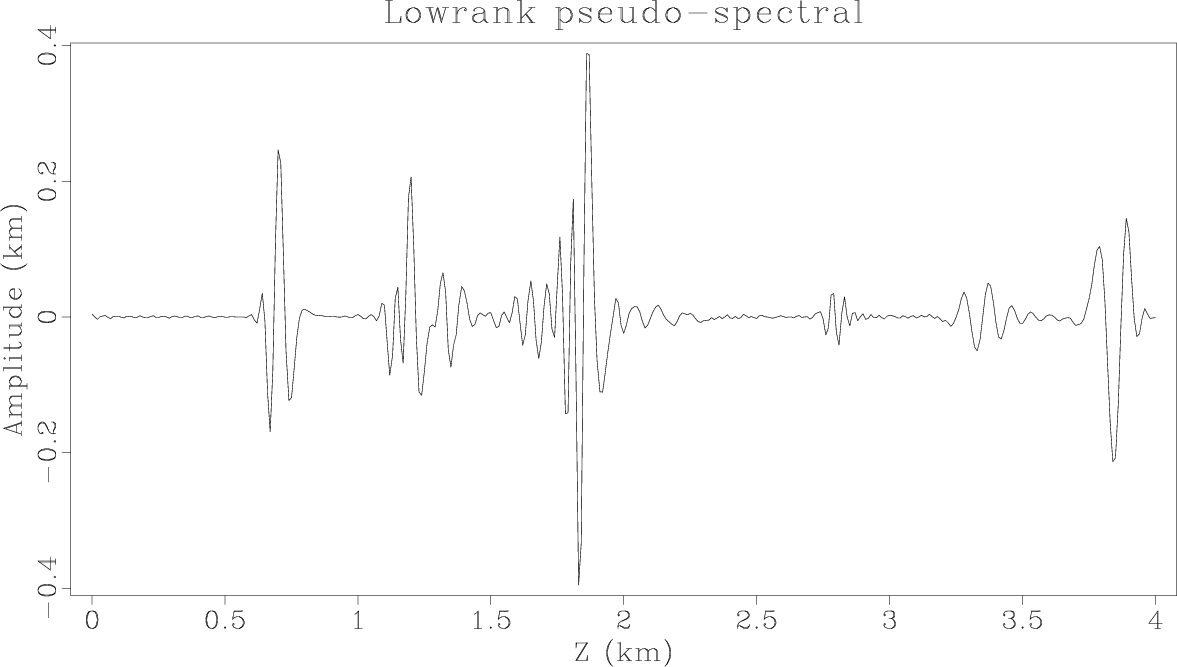
ElasticzFDwave,ElasticzPSLRwave,ElasticzKSSwave
Figure 4. Vertical slices through the vertical components at |
|
|
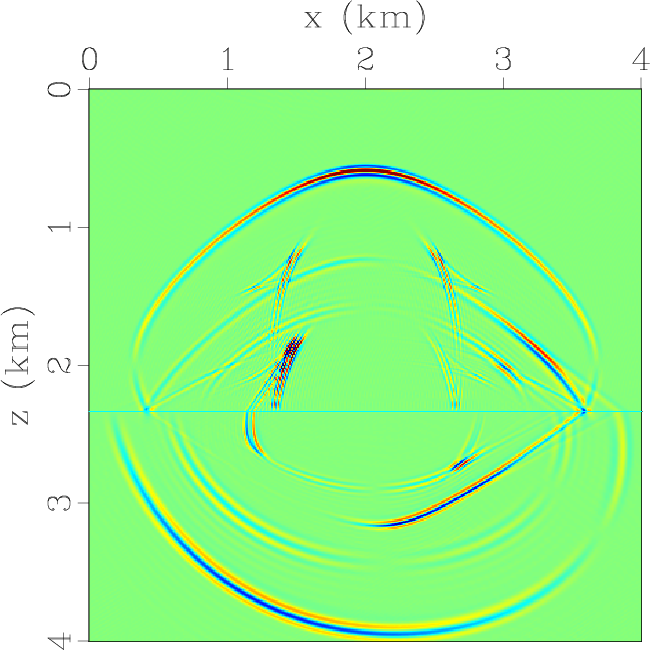
Secondly, we compare two approaches to get the decoupled elastic wavefields
during time extrapolation.
The first approach uses the low-rank pseudo-spectral algorithm
to synthesize the elastic wavefields and then apply the low-rank vector
decomposition algorithm (Cheng and Fomel, 2014) to get the vector qP- and
qSV-wave fields (Figure 5).
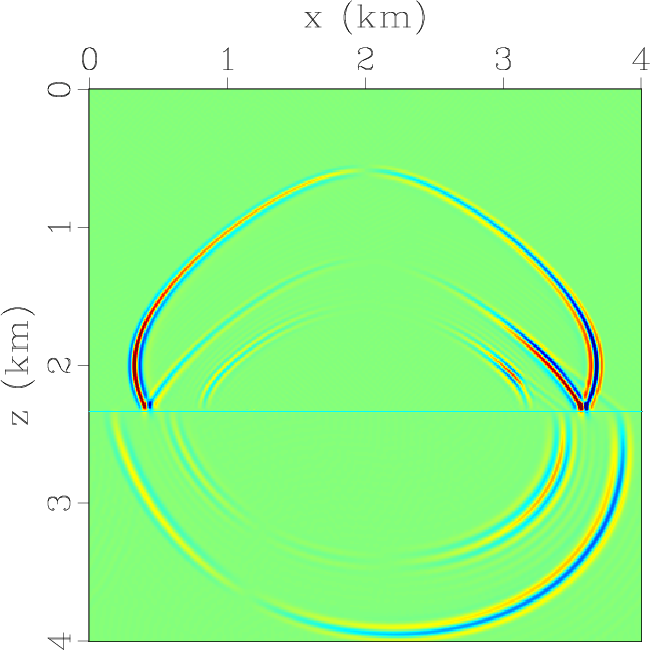
The second extrapolates the decoupled qP- and
qSV-wave fields using the proposed low-rank mixed-domain integral operations (Figure 6).
Extrapolation steps of
![]() m and
m and
![]() ms are used in this example.
The ranks are still
ms are used in this example.
The ranks are still ![]() for the involved low-rank decomposition of the propagation matrices defined in equation 20.
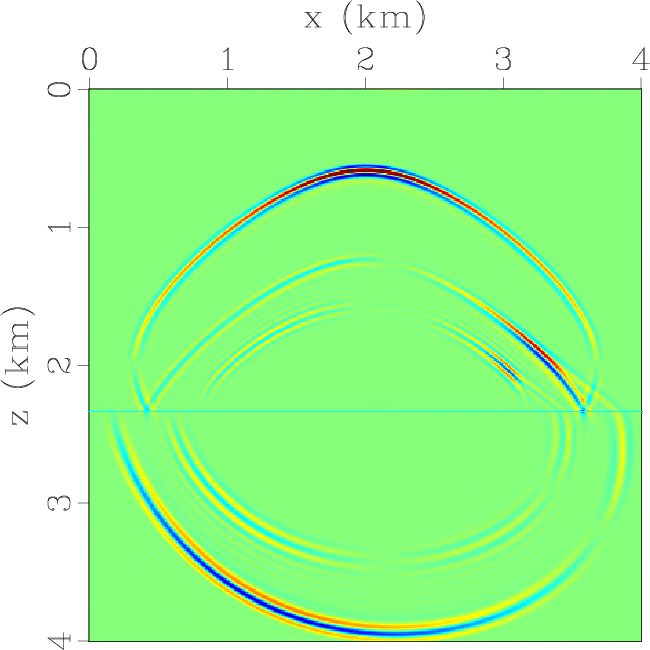
The Two approaches produce comparable elastic wavefields,
in which we can observe all transmitted and reflected waves including mode
conversions.
For one step of time extrapolation, it takes the CPU time of 0.6 ms for the first approach
and 0.5 ms for the second.
This means that merging time extrapolation and vector decomposition into a unified
Fourier integral framework
provides more efficient solution than operating them in sequence
for anisotropic media thanks to the reduced number of forward and inverse FFTs.
for the involved low-rank decomposition of the propagation matrices defined in equation 20.
The Two approaches produce comparable elastic wavefields,
in which we can observe all transmitted and reflected waves including mode
conversions.
For one step of time extrapolation, it takes the CPU time of 0.6 ms for the first approach
and 0.5 ms for the second.
This means that merging time extrapolation and vector decomposition into a unified
Fourier integral framework
provides more efficient solution than operating them in sequence
for anisotropic media thanks to the reduced number of forward and inverse FFTs.

|
|---|
|
ElasticxPSLR1Interf,ElasticzPSLR1Interf,ElasticPxPSLR1Interf,ElasticPzPSLR1Interf,ElasticSxPSLR1Interf,ElasticSzPSLR1Interf
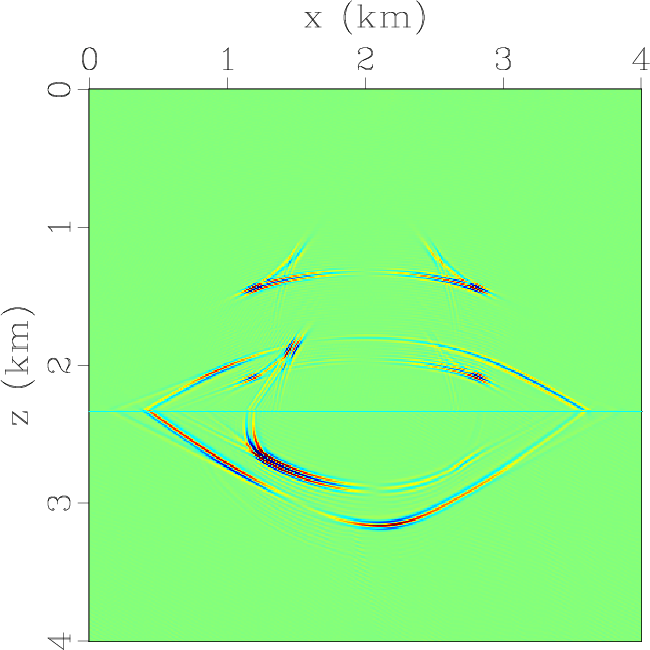
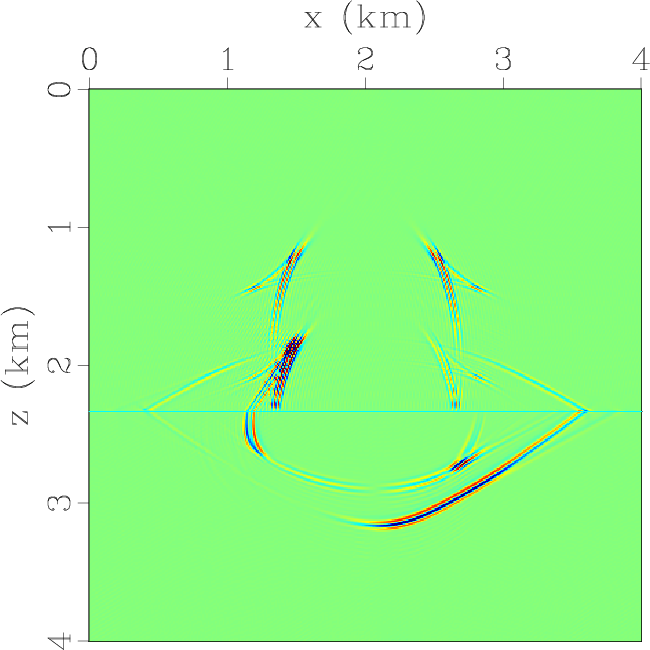
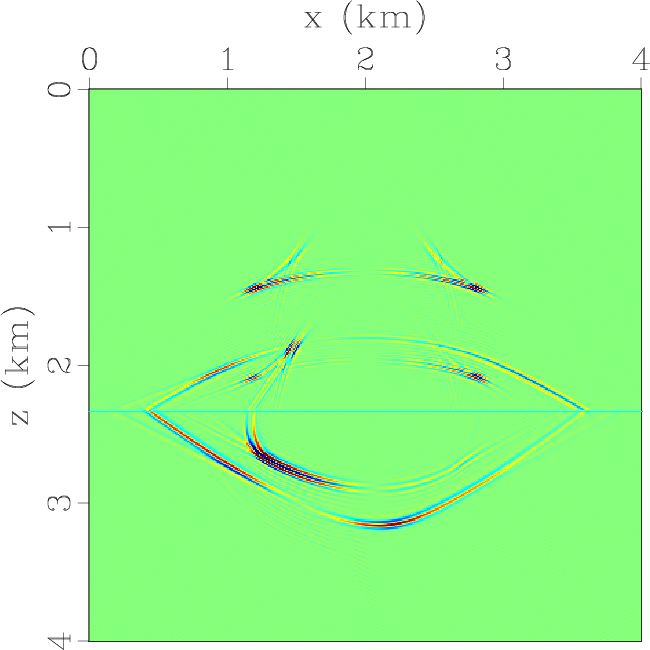
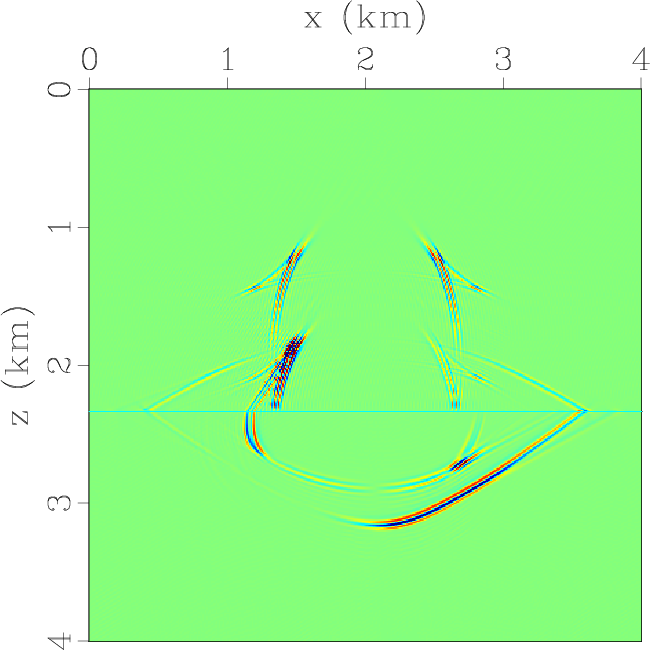
Figure 5. Elastic wavefields at the time of 0.6 s synthesized by using low-rank pseudo-spectral solution of the displacement wave equation followed with low-rank vector decomposition: (a) x- and (b) z-components of the displacement wavefields; (c) x- and (d) z-components of the qP-wave fields; (e) x- and (f) z-components of the qSV-wave fields. |
|
|
|
|---|
|
ElasticPxPSLRInterf,ElasticPzPSLRInterf,ElasticSxPSLRInterf,ElasticSzPSLRInterf,ElasticxPSLRInterf,ElasticzPSLRInterf
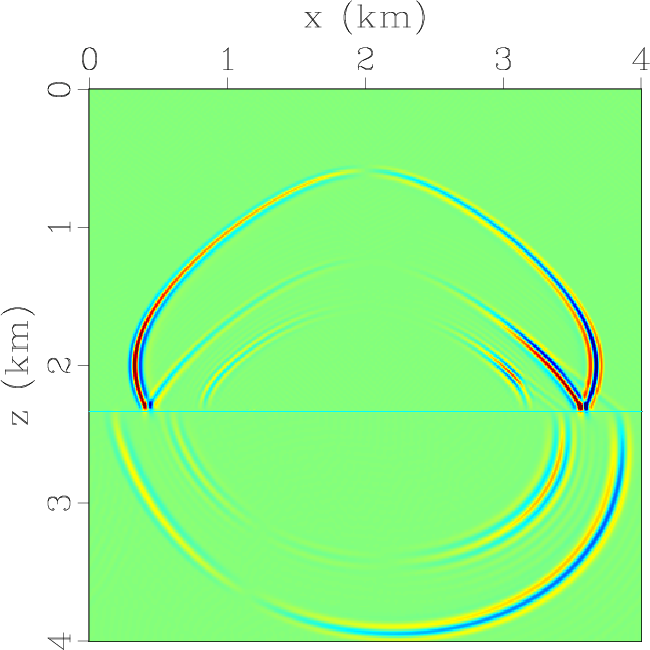
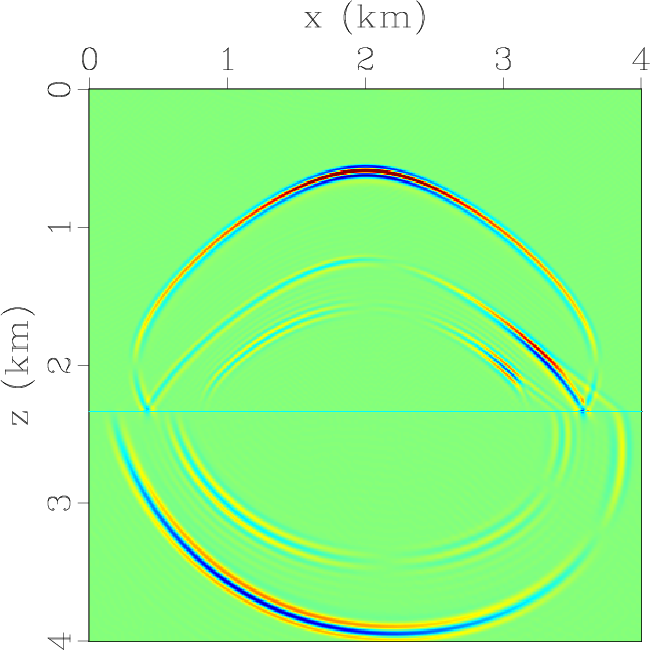
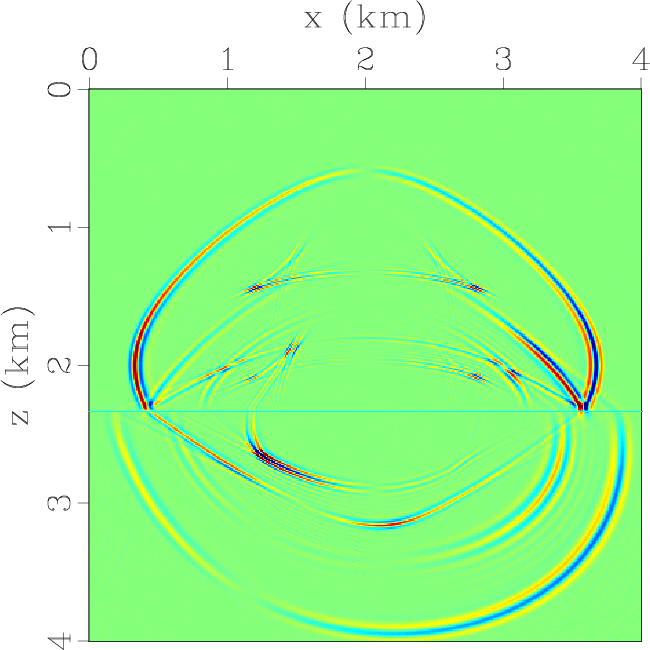
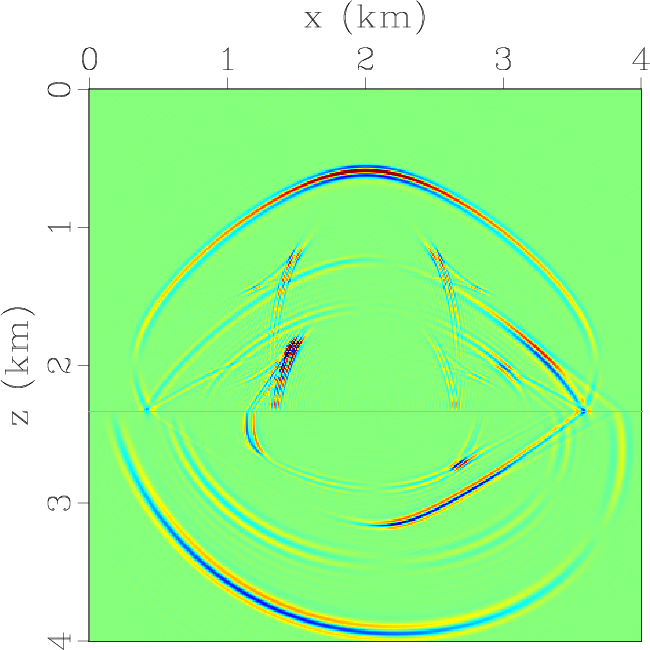
Figure 6. Elastic wavefields at the time of 0.6 s synthesized by using low-rank pseudo-spectral operators for extrapolating and decomposing the elastic waves simultaneously: (a) x- and (b) z-components of the qP-wave displacement wavefields; (c) x- and (d) z-components of the qSV-wave displacement wavefields; (e) x- and (f) z-components of the total elastic wavefields. |
|
|
|
|
|
|
Simulating propagation of decoupled elastic waves using low-rank approximate mixed-domain integral operators for anisotropic media |