|
|
|
|
Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |
This example demonstrates the approach on a two-layer TI model, in which the first layer is a very
strong VTI medium with
![]() ,
,
![]() ,
,
![]() , and
, and
![]() ,
and the second layer is a TTI medium with
,
and the second layer is a TTI medium with
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . The horizontal interface between the two layers
is positioned at a depth of 1.167 km.
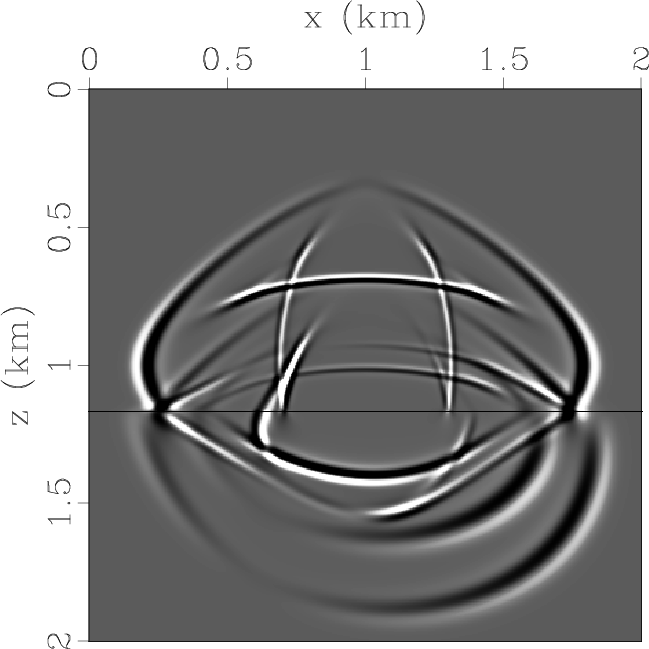
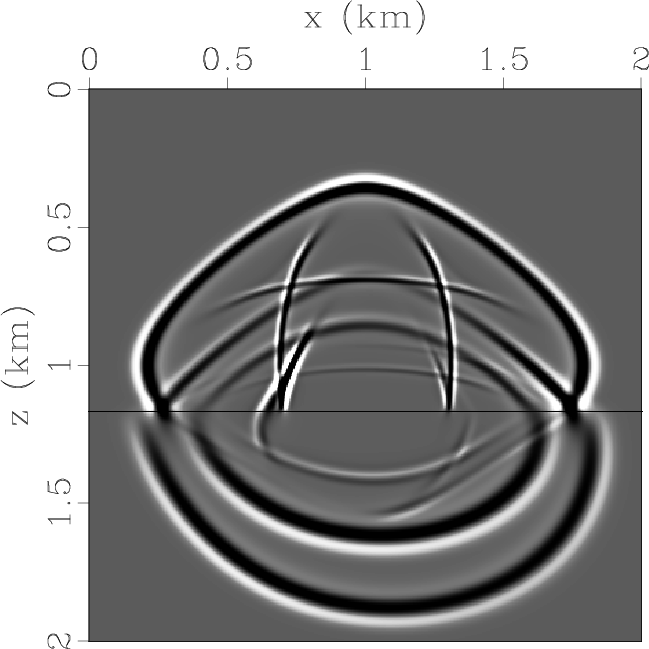
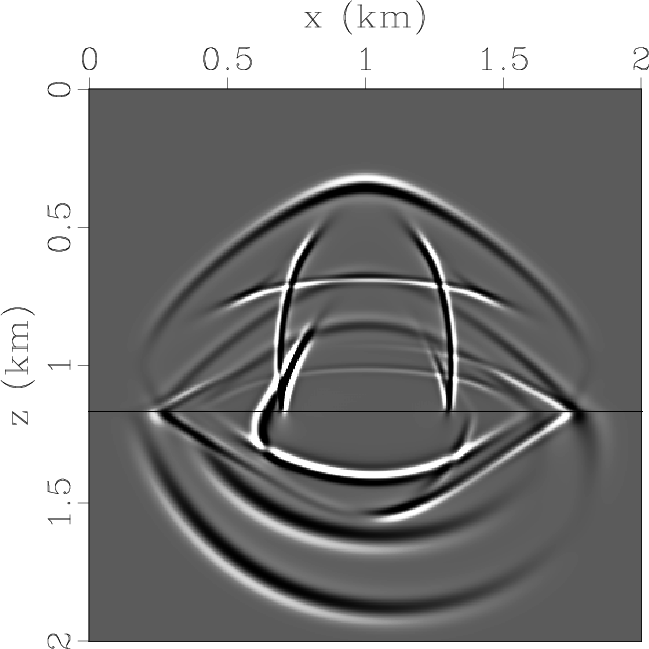
Figure 6a and 6d display the horizontal and vertical components of the displacement wavefields at 0.3 s.
Using the pseudo-pure-mode qP-wave equation, we simulate equivalent wavefields on the same model.
Figure 6b and 6e display the two components of the pseudo-pure-mode qP-wave fields at the same time step.
Figure 6c and 6f display pseudo-pure-mode scalar qP-wave fields and separated qP-wave fields respectively.
Obviously, residual qSV-waves (including transmmited, reflected
and converted qSV-waves) are effectively removed, and all transmitted, reflected as well as converted
qP-waves are accurately separated after the projection deviation correction.
. The horizontal interface between the two layers
is positioned at a depth of 1.167 km.
Figure 6a and 6d display the horizontal and vertical components of the displacement wavefields at 0.3 s.
Using the pseudo-pure-mode qP-wave equation, we simulate equivalent wavefields on the same model.
Figure 6b and 6e display the two components of the pseudo-pure-mode qP-wave fields at the same time step.
Figure 6c and 6f display pseudo-pure-mode scalar qP-wave fields and separated qP-wave fields respectively.
Obviously, residual qSV-waves (including transmmited, reflected
and converted qSV-waves) are effectively removed, and all transmitted, reflected as well as converted
qP-waves are accurately separated after the projection deviation correction.



|
|---|
|
ElasticxInterf,PseudoPurePxInterf,PseudoPurePInterf,ElasticzInterf,PseudoPurePzInterf,PseudoPureSepPInterf
Figure 6. Synthesized wavefields on a two-layer TI model with strong anisotropy in the first layer and a tilted symmetry axis in the second layer: (a) x- and (d) z-components synthesized by original elastic wave equation; (b) x- and (e) z-components synthesized by pseudo-pure-mode qP-wave equation; (c) pseudo-pure-mode scalar qP-wave fields; (f) separated scalar qP-wave fields. |
|
|
|
|
|
|
Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |