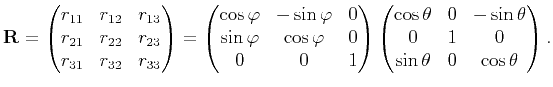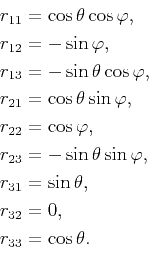|
 |
 |
 | Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |  |
![[pdf]](icons/pdf.png) |
Next: CORRECTION OF PROJECTION DEVIATION
Up: Pseudo-pure-mode qP-wave equation
Previous: Pseudo-pure-mode qP-wave equation in
In the case of transversely isotropic media with a tilted symmetry axis, the elastic tensor loses its simple
form. Written in Voigt notation, it contains nonzero entries in all four quadrants if expressed in global
Cartesian coordinates
 . The generalization of pseudo-pure-mode wave equation to a tilted symmetry
axis involves no additional physics but greatly complicates the algebra. One strategy to derive the wave
equations in TTI media is to locally rotate the coordinate system so that its third axis coincides with
the symmetry axis, and make use of the simple form in VTI media.
. The generalization of pseudo-pure-mode wave equation to a tilted symmetry
axis involves no additional physics but greatly complicates the algebra. One strategy to derive the wave
equations in TTI media is to locally rotate the coordinate system so that its third axis coincides with
the symmetry axis, and make use of the simple form in VTI media.
We introduce a transformation to a rotated coordinate system
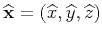 ,
,
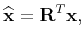 |
(25) |
where the rotation matrix
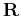 is dependent on the tilt angle
is dependent on the tilt angle 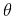 and the azimuth
and the azimuth 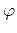 of the
symmetry axis, namely,
of the
symmetry axis, namely,
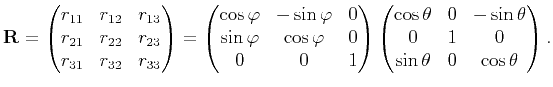 |
(26) |
So,
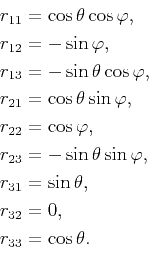 |
(27) |
Assuming that the rotation operator
 varies slowly so that its spatial derivatives can be ignored,
the second-order differential operators in the rotated coordinate system aligned with the symmetry axis are given as:
varies slowly so that its spatial derivatives can be ignored,
the second-order differential operators in the rotated coordinate system aligned with the symmetry axis are given as:
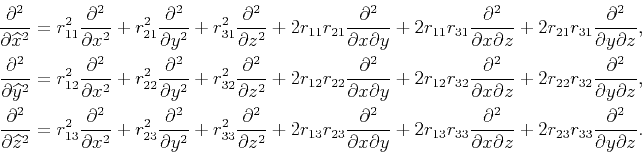 |
(28) |
Substituting these differential operators into the pseudo-pure-mode qP-wave equation of VTI media
yields the pseudo-pure-mode qP-wave equation for TTI media in the global Cartesian coordinates.
Likewise, the pseudo-pure-mode qP-wave equation in TTI media can be further simplified by applying the pseudo-acoustic approximation.
We must mention that, the above
coordinate rotation in deriving the wave equations for TTI and tilted orthorhombic media (see Appendix B)
should be improved to enhance numerical stability according to some significant insights provided in recent literatures
(Macesanu, 2011; Bube et al., 2012; Duveneck and Bakker, 2011; Zhang et al., 2011).
 |
 |
 |
 | Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators |  |
![[pdf]](icons/pdf.png) |
Next: CORRECTION OF PROJECTION DEVIATION
Up: Pseudo-pure-mode qP-wave equation
Previous: Pseudo-pure-mode qP-wave equation in
2014-06-24
![]() . The generalization of pseudo-pure-mode wave equation to a tilted symmetry
axis involves no additional physics but greatly complicates the algebra. One strategy to derive the wave
equations in TTI media is to locally rotate the coordinate system so that its third axis coincides with
the symmetry axis, and make use of the simple form in VTI media.
. The generalization of pseudo-pure-mode wave equation to a tilted symmetry
axis involves no additional physics but greatly complicates the algebra. One strategy to derive the wave
equations in TTI media is to locally rotate the coordinate system so that its third axis coincides with
the symmetry axis, and make use of the simple form in VTI media.
![]() ,
,