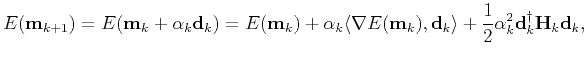|
 |
 |
 | A graphics processing unit implementation of time-domain full-waveform inversion |  |
![[pdf]](icons/pdf.png) |
Next: Nonlinear conjugate gradient method
Up: FWI and its GPU
Previous: FWI and its GPU
In the case of constant density, the acoustic wave equation is specified by
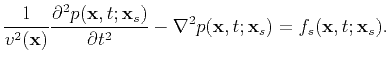 |
(1) |
where we have set
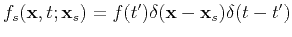 .
According to the above equation, a misfit vector
.
According to the above equation, a misfit vector
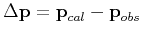 can be defined by the differences at the receiver positions between the recorded seismic data
can be defined by the differences at the receiver positions between the recorded seismic data
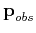 and the modeled seismic data
and the modeled seismic data
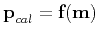 for each source-receiver pair of the seismic survey. Here, in the simplest acoustic velocity inversion,
for each source-receiver pair of the seismic survey. Here, in the simplest acoustic velocity inversion,
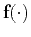 indicates the forward modeling process while
indicates the forward modeling process while
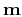 corresponds to the velocity model to be determined. The goal of FWI is to match the data misfit by iteratively updating the velocity model. The objective function taking the least-squares norm of the misfit vector
corresponds to the velocity model to be determined. The goal of FWI is to match the data misfit by iteratively updating the velocity model. The objective function taking the least-squares norm of the misfit vector
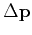 is given by
is given by
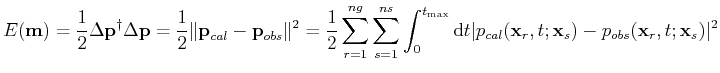 |
(2) |
where 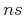 and
and 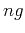 are the number of sources and geophones,
are the number of sources and geophones,  denotes the adjoint operator (conjugate transpose). The recorded seismic data is only a small subset of the whole wavefield at the locations specified by sources and receivers.
denotes the adjoint operator (conjugate transpose). The recorded seismic data is only a small subset of the whole wavefield at the locations specified by sources and receivers.
The gradient-based minimization method updates the velocity model according to a descent direction
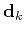 :
:
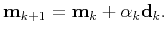 |
(3) |
where 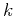 denotes the iteration number. By neglecting the terms higher than the 2nd order, the objective function can be expanded as
denotes the iteration number. By neglecting the terms higher than the 2nd order, the objective function can be expanded as
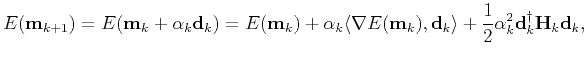 |
(4) |
where
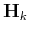 stands for the Hessian matrix;
stands for the Hessian matrix;
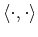 denotes inner product. Differentiation of the misfit function
denotes inner product. Differentiation of the misfit function
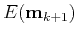 with respect to
with respect to 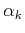 gives
gives
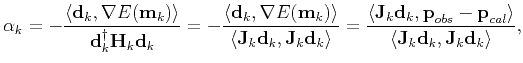 |
(5) |
in which we use the approximate Hessian
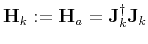 and
and
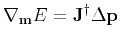 , according to equation (A-7). A detailed derivation of the minimization process is given in Appendix A.
, according to equation (A-7). A detailed derivation of the minimization process is given in Appendix A.
 |
 |
 |
 | A graphics processing unit implementation of time-domain full-waveform inversion |  |
![[pdf]](icons/pdf.png) |
Next: Nonlinear conjugate gradient method
Up: FWI and its GPU
Previous: FWI and its GPU
2021-08-31
![]() :
: