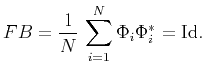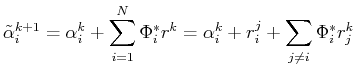|
 |
 |
 | Seislet-based morphological component analysis using scale-dependent exponential shrinkage |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Yang & Fomel: Seislet-based
Previous: Acknowledgments
Connections between seislet frame and seislet-MCA algorithm
The complete data 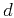 is regarded to be superposition of several different geometrical components, and each component can be sparely represented using a seislet dictionary
is regarded to be superposition of several different geometrical components, and each component can be sparely represented using a seislet dictionary 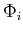 , i.e.,
, i.e.,
![\begin{displaymath}\begin{array}{ll} d&=\displaystyle \sum_{i=1}^N d_i=\sum_{i=1...
... \alpha_2\\ \vdots\\ \alpha_N \end{array} \right]\\ \end{array}\end{displaymath}](img100.png) |
(29) |
where
![$ F=[\Phi_1,\Phi_2,\cdots,\Phi_N]$](img101.png) is a combined seislet dictionary (i.e. seislet frame), and the backward operator is chosen to be
is a combined seislet dictionary (i.e. seislet frame), and the backward operator is chosen to be
![$\displaystyle B=\frac{1}{N}\,\left[\begin{array}{l} \Phi_1^{*}\\ \Phi_2^{*}\\ \vdots\\ \Phi_N^{*} \end{array} \right]$](img102.png) |
(30) |
in the sense that
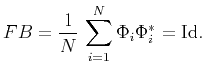 |
(31) |
The difference between seislet-MCA algorithm and seislet frame minimization is the use of BCR technique (Bruce et al., 1998): We sparsify one component while keeping all others fixed. At the 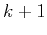 -th iteration applying the backward operator on the
-th iteration applying the backward operator on the 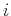 -th component leads to
-th component leads to
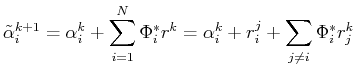 |
(32) |
where the terms
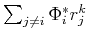 are the crosstalk between the
are the crosstalk between the 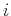 -th component and the others. An intuitive approach to filter out the undesired crosstalk is shrinkage/thresholding. The proposed exponential shrinkage provides us a flexible control on the performance of the shrinkage/thresholding operator.
-th component and the others. An intuitive approach to filter out the undesired crosstalk is shrinkage/thresholding. The proposed exponential shrinkage provides us a flexible control on the performance of the shrinkage/thresholding operator.
 |
 |
 |
 | Seislet-based morphological component analysis using scale-dependent exponential shrinkage |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Yang & Fomel: Seislet-based
Previous: Acknowledgments
2021-08-31
![]() is regarded to be superposition of several different geometrical components, and each component can be sparely represented using a seislet dictionary
is regarded to be superposition of several different geometrical components, and each component can be sparely represented using a seislet dictionary ![]() , i.e.,
, i.e.,
![\begin{displaymath}\begin{array}{ll} d&=\displaystyle \sum_{i=1}^N d_i=\sum_{i=1...
... \alpha_2\\ \vdots\\ \alpha_N \end{array} \right]\\ \end{array}\end{displaymath}](img100.png)
![$\displaystyle B=\frac{1}{N}\,\left[\begin{array}{l} \Phi_1^{*}\\ \Phi_2^{*}\\ \vdots\\ \Phi_N^{*} \end{array} \right]$](img102.png)